Overview

The goal of our research is to design and implement a distributed algorithm for localizing nodes in a sensor network. That is, compute the 2D or 3D position of each node relative to each other. We formulate the problem as the two-dimensional graph realization problem: given a planar graph with approximately known edge lengths, recover the Euclidean position of each vertex up to a global rotation, translation, and possible reflection. This formulation is applicable to the localization of sensor networks in which each node can estimate the distance to its neighbors, but no absolute position reference such as GPS or fixed anchor nodes is available.

We introduce the notion of robust quadrilaterals in order to label certain subgraphs as rigid and uniquely localizable even when the network as a whole may not have a unique realization. We propose a distributed algorithm that finds robust subgraphs of the input graph, and solves for position estimates by connecting these subgraphs in a way that is tolerant to distance measurement noise. Our algorithm runs in linear time with the number of nodes in the network, assuming all nodes have O(1) neighbors. The algorithm handles arbitrary measurement noise by adjusting its robustness parameters. In addition to the node positions, the algorithm also computes error bounds for each position estimate so that the algorithm and user are fully aware of any localization uncertainty. An implementation of the algorithm is demonstrated to produce accurate localizations for a variety of graphs, including those arising from real-world node placement strategies [1].

Purpose

Robust localization is a valuable tool for the development of low-cost sensor networks for use in location-aware applications and ubiquitous networking [2]. Reliable position information can be used by higher level applications such as person or object tracking within an environment, autonomous robot navigation, or novel human-computer interfaces. An inexpensive, scalable localization system is desirable to make existing sensor networks location-aware with minimal changes.

The majority of previous research on network localization assumes that some nodes have prior knowledge of their position, either from manual initialization or an outside data source such as GPS [3]. These anchor nodes are then used as a reference point when estimating the position of other nodes. Our algorithm seeks to eliminate the requirement for anchor nodes, allowing complete mobility and ease of deployment.

Approach

At a high level, our network localization algorithm works as follows. Each node measures distances to neighboring nodes and then shares these measurements with its neighbors. We then find all sets of four nodes that are fully connected by distance measurements and are "well-spaced" such that even in the presence of measurement noise, their relative positions are unambiguous. We adopt this 4-vertex quadrilateral as the smallest subgraph that can be uniquely realized, and define it as robust. Additional 4-vertex quads can be "chained" to the original quad if they have 3 nodes in common with it. This approach allows each chained quad to localize its fourth node based on the 3 known positions common to the two quads. Figure 1 depicts an illustrative run of our algorithm.

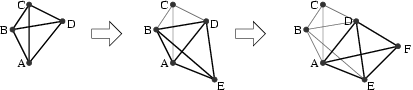
Figure 1 An example run of our algorithm to estimate the relative positions of node A's neighbors. Nodes ABCD are robust because their realization is unambiguous even in the presence of noise. In the next stage, node E is localized relative to the known positions of ABCD. Continuing, the same procedure is used to localize node F which is part of the super-rigid quad ADFE.

A key innovation of this paper is the use of the 4-vertex robust quadrilateral as a means to tolerate noise, enabling our algorithm to compute unique realizations for graphs that might otherwise be ambiguous. Another important feature of our algorithm is that each cluster (consisting of a node and its neighbors) is localized in its own coordinate system. Clusters can then be connected by chaining coordinate transformations in an on-line fashion to localize nodes several hops apart.

Results

We have tested our algorithm on both large-scale simulated networks and medium-scale physical networks in order to evaluate its performance under varying amounts of noise, node connectivity, mobility, and environment shapes. Localization results for a simulated network are shown in Figure 2, consisting of a simple two-dimensional square region 15 meters on a side. One hundred nodes are placed uniformly and randomly in the region and each node can measure the distance to any node within a specified distance. Gaussian noise with a fixed variance is added to all distance measurements.

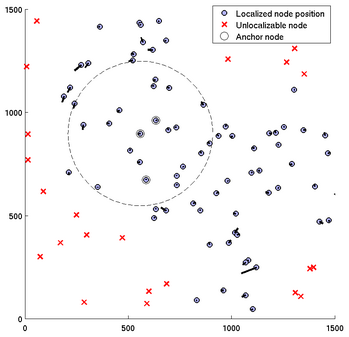
Figure 2 A simulated network localized by our algorithm. Note that some nodes, represented by red X's, were not localizable due to lack of robustness. The dashed circle indicates the maximum communications radius of one node. Black lines indicate the difference between ground truth and localized position.

For physical experiments, we make use of a platform for sensor network experimentation, the Cricket location-support system, also developed at MIT. Crickets are equipped with a microprocessor, a Radio Frequency (RF) transmitter and receiver, and an ultrasonic transducer and receiver. Inter-node distances can be computed to an accuracy of approximately 1 centimeter by measuring the Time of Arrival (ToA) of an ultrasound pulse. The on-board microprocessor of a Cricket is sufficiently powerful to implement our localization algorithm on-board using TinyOS, enabling a truly distributed sensor network. Figure 3 shows a video of the network localization in action on a real sensor network.

Figure 3 A video (click to play) showing the real-time localization of a sensor network, including the tracking of a mobile robot with the same algorithm.

Our TinyOS implementation of the algorithm and simulation resources have been made freely available for other researchers.

Future Work

Our future research will focus on two main areas: Physical realization of a practical self-localizing sensor network and greater understanding of the error characteristics in such a network. In the first area, we are collaborating with other research groups at MIT to pursue the use of Ultrawideband (UWB) radio for an accurate and scalable sensor network ranging capability. The second area of future research is being pursued through a more rigorous application of probability theory to our algorithm. Lastly, a useful extension of this work is use robustness as a means to compute the optimal placement of additional nodes so that network deployment may be motivated for maximum localization accuracy.

Research Support

This work was funded by a grant from Project Oxygen and supported in part by a National Science Foundation Graduate Research Fellowship. Additional funding was provided in part by the Institute for Security Technology Studies (ISTS) at Dartmouth College, NSF award 0225446, ONR awards N00014-01-1-0675, N00014-02-C-0210, and N00014-03-1-0879, and DARPA TASK program award F30602-00-2-0585.

References

[1] David Moore, John Leonard, Daniela Rus and Seth Teller. Robust Distributed Network Localization with Noisy Range Measurements. In Proceeedings of the Second ACM Conference on Embedded Networked Sensor Systems (SenSys '04), pp. 50--61, Baltimore, MD, November 2004.

[2] Seth Teller, Jiawen Chen, and Hari Balakrishnan. Pervasive pose-aware applications and infrastructure. IEEE Computer Graphics and Applications, pp. 14--18, July/August 2003.

[3] Lance Doherty, Kristofer S. J. Pister, and Laurent El Ghaoui. Convex position estimation in wireless sensor networks. In Proceedings of IEEE Infocom, Anchorage, AK, April 2001.