Introduction

Currently, robotics research has shown that robots are capable of performing many complex and useful tasks. For example, Robonaut, a humanoid robot developed at Johnson Space Center, is capable of performing many of the tasks currently performed by astronauts, such as space-truss assembly, EVA setup and teardown, Shuttle tile inspection, and ISS maintenance and repair operations (Ambrose, Culbert, and Rehnmark 2001) (Fredrickson, Lockhart, and Wagenknecht 1999). At present, however, Robonaut can only perform these tasks in the controlled and predictable environment of the laboratory. For robots such as Robonaut, dealing with the uncertainties and disturbances inherent to uncontrolled environments compounds the already difficult problem of performing these complex tasks.

To help robots deal with uncertainties and disturbances, the automated planning community has developed temporally flexible planners, such as KIRK (Kim et al. 2001) and HSTS (Muscettola et al. 1998), and continuous planners, such as ASPEN (Rabideau et al. 1999). Temporally flexible planners are able to adapt to perturbations in execution time without breaking the entire plan. These planners only impose those temporal constraints required to guarantee a plan’s success, leaving flexibility in the execution time of activities. This flexibility is then exploited, in order to adapt to uncertainty, by delaying the scheduling of each activity until it is executed. Continuous planners are capable of quickly generating a new plan as soon as an environment change breaks the current mission plan. A downside of these continuous planners is that they do not allow for temporal flexibility in the execution time of activities, as they assign hard execution times to activities.

Current research by (Shu, Effinger, and Williams 2005) aims to combine these two approaches by augmenting temporally flexible planning with the ability to update temporally flexible plans incrementally as uncertainties and disturbances arise. This is accomplished by identifying and changing only the inconsistent portions of the plan, instead of developing a whole new plan. Empirical studies of this approach demonstrate an order of magnitude speed increase in temporally flexible planning.

Background

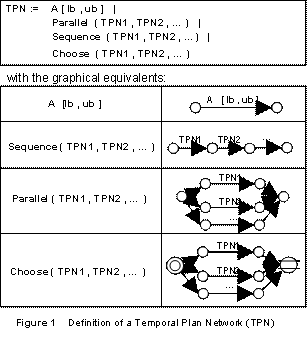
The standard definition of a temporally flexible plan specifies predecessor and successor relations between activities, and simple temporal constraints that relate the start and end times of activities. In the approach described above, we augment the temporally flexible plan by introducing choice nodes. We call the augmented temporally flexible plan a temporal plan network (TPN).

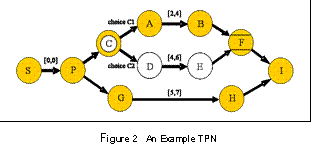
In a TPN, shown in Figure 1, a choice between alternative courses of action is represented by a choice start node, (represented by a double circle), a choice end node (represented by a circle with two parallel lines), and alternative subplans between them. Figure 2 shows an example TPN with a parallel set of activities branching at node P and converging at node F. The example TPN also has a choice between two possible subplans, C1 and C2.

Roughly speaking, a temporally flexible planner can choose a candidate plan from the TPN by choosing one and only one execution path thru each of the choice start and choice end nodes in the TPN. Therefore, a TPN represents a family of closely related plans, and corresponding STNs, that consist of all possible permutations of choices that can be made in the TPN. For example, the TPN in Figure 2 represents two closely related plans, one corresponding to the plan in the figure when choice C1 is selected, and one corresponding to the plan in the figure when choice C2 is selected.

Problem Formulation

Interestingly, the TPN can be translated directly into a temporal Conditional CSP. This analogous representation allows one to think of the temporally flexible planning problem as directly analogous to solving a conditional constraint satisfaction problem, in which the conditional variables are the choice nodes, the conditions describe the upstream relationship between choice nodes, and the constraints are simple temporal constraints.

The advantage of this transformation is that very fast and sophisticated search techniques have been developed to solve conditional CSPs (Gelle 2003). One such search technique is to use conflicts to guide the search. There are several conflict-directed CSP search algorithms in the literature. Three of the most popular are Conflict-Directed Backjumping (Prosser 1993), Dynamic Backtracking (Ginsberg 1993) and Conflict-directed A* (Williams and Ragno 2002). For example, Dynamic Backtracking ensures a complete, systematic, and memory-bounded search, while leveraging conflicts to only generate candidate plans that resolve all known conflicts. In addition, dynamic backtracking performs dynamic variable reordering in order to preserve assignments, when possible. In order to frame search through the TPN as conflict-directed search on a conditional CSP, we have implementated a straightforward generalization of Dynamic Backtracking that is extended to handle conditional variables.

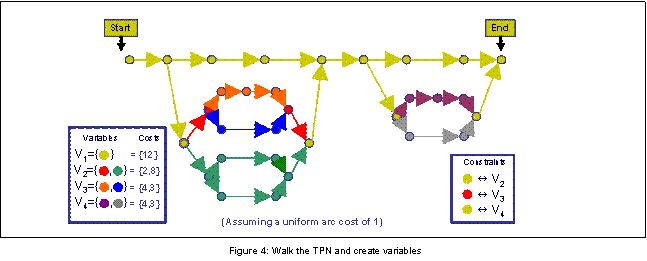
The pseudocode of the translation from a TPN to a conditional CSP is presented in Figure 3, and an example is provided in Figure 4. Notice in this example that timebounds are not included on the arcs. This is because timing constraints are not considered when initially grouping the nodes and arcs to form a conditional CSP. They are used, however, when testing if a particular variable-value assignment to the conditional CSP is consistent. As seen in Figure 4, assigning costs to variable-value assignments in the conditional CSP is straightforward. Assuming, without loss of generality, a uniform arc cost of 1, the cost of a particular variable-value pair corresponds to the sum of all arc’s costs that are grouped with that variable-value assignment. In Figure 4, each variable-value assignment corresponds to a particular color. Additionally, each conditional constraint is represented as a double implication between a particular value (or color), and a variable that must then subsequently be assigned a value (or color).

Problem Statement

A next direction for this research is to efficiently extract minimal conflicts so the conflict-directed candidate plan generator can effectively guide the search. Previous work, (Shu, Effinger, and Williams 2005) has enabled incremental conflict-extraction and inconsistency resolution on simple temporal networks with the ITC algorithm, which stands for Incremental Temporal Consistency. The conflicts generated by ITC are then fed into a conflict-directed candidate generator to efficiently generate candidate plans.

A key observation emanating from this work is that even though the conflict returned by ITC is minimal with respect to the inconsistent candidate STN in which it was found, this conflict is not necessarily minimal with respect to the Temporal Plan Network from which this inconsistent candidate STN arose. This is an important observation, because feeding non-minimal conflicts into a conflict-directed search routine, significantly slows down the search to approach that of chronological backtracking. This undesirable loss of efficiency, however, can be avoided by ensuring that the conflicts fed into the candidate generator are minimal.

After an initial investigation, we believe non-minimal conflicts returned by ITC can be minimized by a fast algorithm that is linear in the size of the conflict returned by ITC. A portion of the pseudocode for this conflict minimization idea is presented in Figure 5. We hope that this conflict-minimization algorithm will enable significantly more focused conflict-directed candidate generation of temporally flexible plans. This seems promising, since a conflict-directed search algorithm that is fed minimal conflicts will generate less candidate plans, by only generating candidate plans that resolve all known conflicts.

Only the top-level of the extractMinimalConflict pseudocode is provided below, and a discussion of its functionality must be postponed until the author does more work. :)

Acknowlegements

This research is supported by the NASA IS program under contract NCC-2-1235.

References

[1] Ambrose, R., Culbert, C., and Rehnmark, “An experimental investigation of dexterous robots using EVA tools and Interfaces", In AIAA Space 2001, Albequerqe, NM.

[2] Fredrickson, S.E., Lockhart, P.S., and Wagenknecht, J.D. “Autonomous extravehicular robotic camera (AERCam) for remote viewing. In AIAA ISS-SVC 1999, Houston, TX

[3] Gelle, E. and Sabin M., 2003. Solving Methods for Conditional Constraint Satisfaction. In IJCAI-2003.

[4] Ginsberg, M.L., 1993. Dynamic backtracking. In Journal of AI Research, 1:25-46.

[5] Kim, P.; Williams, B.; and Abrahmson, M, 2001. Executing Reactive, Model-based Programs through Graph-based Temporal Planning. In IJCAI-2001.

[6] Muscettola N., et al., 1998. Issues in temporal reasoning for autonomous control systems. In Autonomous Agents 1998.

[7] Prosser, P., 1993. Hybrid algorithms for the constraint satisfaction problem, In Comp. Intelligence. 3, 268-299.

[8] Shu, I., Effinger, R., and Williams, B., 2005. Enabling Fast Flexible Planning through Incremental Temporal Reasoning with Conflict Extraction. In ICAPS05 .

[9] Rabideau, G., et.al., 1999. Iterative Repair Planning for Spacecraft Operations in the ASPEN System. In ISAIRAS 1999 .

[10] Williams, B. and Ragno, J., 2002. Conflict-directed A* and its role in model-based embedded systems. In Journal of Discrete Applied Math 2002.