Approximate Inference for Graphical Models

Jason K. Johnson & Alan S. Willsky

The Problem

A graphical model is a probabilistic model for a collection of random variables defined on a graph with vertices and edges . Each vertex of the graph is associated with a random variable and each edge represents a statistical dependency between variables and . The joint probability distribution of all variables is encoded as a product of potential functions

where each potential encodes the interaction among a subset of variables which are fully connected in the graph (otherwise, ).

An important inference problem which arises for these models is to calculate certain summary statistics for each variable. For instance, we may be interested in the marginal probability distribution of a single variable

which involves integrating or summing over all possible values of the other variables. However, extracting these marginal statistics of individual variables can require enormous computation in models with many variables and complex graphical structure. Hence, there is a need for tractable approximation methods for graphical models for which exact computations are prohibitively complex.

Our Approach

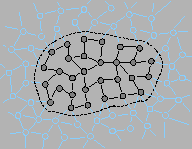
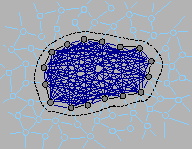
Our approximate inference algorithm is based on two basic components: (1) variable elimination and (2) model reduction.

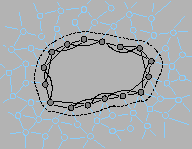
(1) Variables are eliminated from a graphical model by summing or integrating the product potential over all possible values of the variables being eliminated. While this reduces the number of variables in the model, it can also have the discouraging effect of inducing many additional interactions between the neighbors of the eliminated variables. This tends to spoil the sparsity of the graphical model complicating further variable elimination calculations so that exact inference can become intractable in larger models.

(2) To overcome this difficulty we apply Occam's razor. When the "boundary model" induced by variable elimination becomes overly complicated, we "project" that intractable boundary model into a class of simpler models having fewer interactions between variables. This involves a greedy algorithm to select model structure and a convex optimization procedure to minimize modeling error (Kullback-Leibler divergence) within the family of probability models having that simplified model structure.

Employing a "divide and conquer" approach to inference, together with a particular strategy for alternating between variable elimination and model reduction, we are able to develop fast recursive inference methods which approximately compute the marginals of a graphical model.

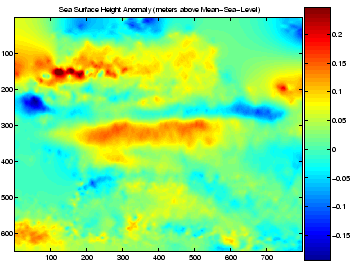
Remote-Sensing Application

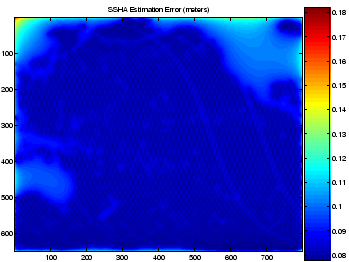
We have applied our approach to perform near-optimal interpolation of satellite altimetry measurements of sea-surface height anomaly (relative to mean-sea-level). We presume a prior model for the sea-surface anomaly which is a discretized Gaussian process with nearest-neighbor interactions between adjacent random variables on a 2-D grid. Conditioned on sparse and noisy altimetry measurements, we compute approximate marginals at each grid point to obtain smoothed and interpolated images of the expected sea-surface height anomaly as a function of latitude and longitude and an associated spatially-varying measure of uncertainty. Below, we show these results for the Pacific ocean basin based on data collected over a 10-day period in November of 2004.

Future Work

Thus far, we have applied our approximate inference framework for Gaussian models defined on 2-D nearest-neighbor models. We plan to extend this work to multiresolution models of processes for which nearest-neighbor models are inadequate to capture global correlations of the process. We also plan to implement this framework for approximate computation of marginals probabilities in discrete models and to explore similar approximate dynamic programming methods for estimating the most-probable configuration of a discrete model.

Acknowledgements

The authors gratefully thank Shell for their support of this research.

References

[1] J.K. Johnson. MS Thesis: Estimation of GMRFs by Recursive Cavity Modeling. MIT, March 2003.

[2] J.K. Johnson, A.S. Willsky. A Recursive Model-Reduction Method for Approximate Inference in Gauss-Markov Random Fields. in preparation, April 2005.