What

We have developed a technique for planning in large, real-world problems in the presence of substantial uncertainty. Our algorithms find control policies that can avoid ambiguous situations by taking advantage of information implicit in the world, and can also resolve uncertainty by taking advantage of information-gathering actions.

Why

Recent research in the field of robotics has demonstrated the utility of probabilistic models for perception and state tracking on deployed robot systems. For example, Kalman filters and Markov localisation have been used successfully in many robot applications [3,5]. There has also been considerable research into control and decision making algorithms that are robust in the face of specific kinds of uncertainty [1]. Few control algorithms, however, make use of full probabilistic representations throughout planning. As a consequence, robot control can become increasingly brittle as the system's perceptual uncertainty, and state uncertainty, increase.

The Partially Observable Markov Decision Process (POMDP) is a way to model uncertainty in a real world system's actions and perceptions [4]. Instead of making decisions based on the current perceived state of the world, the POMDP maintains a belief, or probability distribution, over the possible states of the world, and makes decisions based on the current belief. POMDPs are unfortunately computationally intractable for most real world problems involving planning in belief spaces.

How

The uncertainty that many real world problems exhibit often has a regular structure that can be exploited. By making assumptions about the kinds of probability distributions that a system may experience, it may be possible to reduce the complexity of finding policies that approximate the optimal POMDP policy, without being subject to the pain of finding the exact optimal policy. In figure 1 below we see two example beliefs, shown as particles drawn from the probability distribution over the possible locations of a mobile robot in a map. The denser the particles, the more likely the robot is to be at or near that location. On the left is the kind of distribution that could reasonably be expected to occur; the true location of the robot is not known but is relatively constrained. The right-hand image, however, shows particles drawn from a very unlikely distribution. An algorithm that ignores such beliefs during planning will still perform well in the real-world. By ignoring such unlikely beliefs, we are able to generate good policies (in terms of expected reward) in a computationally tractable way. This allows for more reliable control in a number of situations, from motor control to system diagnosis. We have demonstrated this approach on both mobile robot motion planning and speech dialogue management.

Figure 1:Two example probability distributions over where a robot might be. On the left is the kind of distribution that could reasonably be expected to occur. On the right is a distribution that is very unlikely.

Our ability to produce good policies for POMDP-style problems relies on using compact representations of the probabilistic state estimates. One algorithm uses a hand-chosen set of statistics: the mean and entropy. These statistics are jointly sufficient under certain restricted classes of distributions, for example, gaussians with a single variance parameter. For other distributions, this representation can be viewed as lossy. A second algorithm demonstrates a way to find low-dimensional representations of a set of high-dimensional probability distributions automatically, through a technique similar to Principal Components Analysis (PCA). PCA is a technique for finding some low-dimensional, linear subspace that passes through, or close to, a set of data. The particular distance metric used by conventional PCA is not well-suited for representing probability distributions; however, PCA can be easily modified for other distance metrics. We have demonstrated how to modify PCA appropriately for probability distributions, a technique called exponential-family PCA (E-PCA) [2], and how to plan using this representation.

Progress

Figure 2 compares the approximate POMDP solution with a conventional distance-optimal algorithm. The objective is for the robot to travel from the start to the goal location, with limited sensing. Not shown is the full probability distribution at each point in time. However, the conventional, distance-optimal motion planning algorithm becomes very uncertain about its position and ultimately lost, because the distance-optimal trajectory causes the robot to be without sensor information for an extended period of time. In contrast, the POMDP-style solution is able to model the limited sensing, and chooses a trajectory that compensates for the limited sensing range by following the walls. As a result, the robot is able to reach the goal robustly.

Figure 2: Two example motion trajectories for a robot with limited sensing ability. On the left is the conventional distance-optimal trajectory that fails to reach the goal. On the right is the approximate POMDP trajectory that reaches the goal.

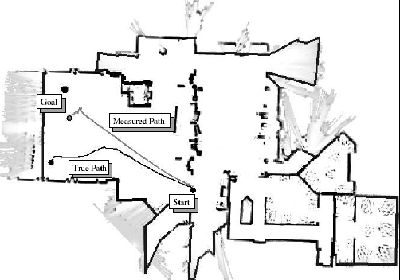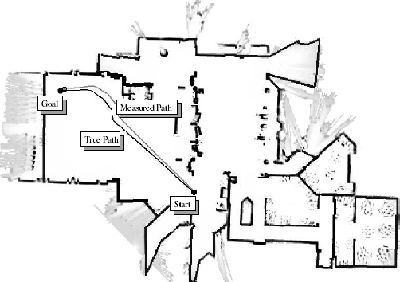[Conventional Policy ]	[Approx. POMDP Policy]

Research Support

This research was supported in part by the National Science Foundation under ITR grant # IIS-0121426.

Acknowledgements

This is joint work with Sebastian Thrun and Geoffrey Gordon.

References

[1] J. Andrew Bagnell and Jeff Schneider. Autonomous helicopter control using reinforcement learning policy search methods. pages 1615--1620, Seoul, South Korea, 2001. IEEE Press.

[2] Michael Collins, Sanjoy Dasgupta, and Robert Schapire. A generalization of principal components analysis to the exponential family. In T. G. Dietterich, S. Becker, and Z. Ghahramani, editors, Advances in Neural Information Processing Systems 14 (NIPS), Cambridge, MA, 2002. MIT Press.

[3] John Leonard and Hugh Durrant-Whyte. Mobile robot localization by tracking geometric beacons. IEEE Transactions on Robotics and Automation, 7(3):376--382, June 1991.

[4] Edward Sondik. The Optimal Control of Partially Observable {M}arkov Decision Processes. PhD thesis, Stanford University, Stanford, California, 1971.

[5] Sebastian Thrun, Michael Beetz, Maren Bennewitz, Wolfram Burgard, Armin B. Cremers, Frank Dellaert, Dieter Fox, Dirk Haehnel, Charles Rosenberg, Nicholas Roy, Jamieson Schulte, and Dirk Schulz. Probabilistic algorithms and the interactive museum tour-guide robot minerva. International Journal of Robotics Research}, 19(11):972--999, November 2000.