Diagnosis as Approximate Belief State Enumeration for Probabilistic Concurrent Constraint Automata
Oliver B. Martin & Brian C. Williams
The purpose of estimation is to determine the current state of the system. An estimator infers the current state by reasoning over a model of the system dynamics along with the commands that have been executed and the resulting sensory observations. In many embedded systems, this knowledge of the current state is then used by a controller to drive the system state towards a specific target or goal. The ability for a system to accurately and reliably deduce its current state can dictate whether it is able to achieve its objectives. This is particularly important for highly complex robotic space exploration systems that operate in uncertain environments. Furthermore, deep space communication delays and severely constrained onboard computing capabilities present tremendous challenges to traditional methods of estimation in support of robust autonomous spacecraft operations.
Challenge
Unfortunately, within the model-based programming paradigm, complete online mode estimation for any realistic system is intractable due to the combinatorial nature of concurrently operating components. Even a simplified Mars Entry Decent and Landing (EDL) subsystem [3], similar to the one used for the MER rovers operating on Mars, has 10 components with an average of 4.4 modes per component. When modeled as a Probabilistic Concurrent Constraint Automata (PCCA), the complete belief state is 4.410 and already too large to fully enumerate online. Fortunately, the vast majority of the belief state is probabilistically sparse and maintaining only a few leading estimates can capture the true behavior of the system with a high level of confidence.
Previous Work
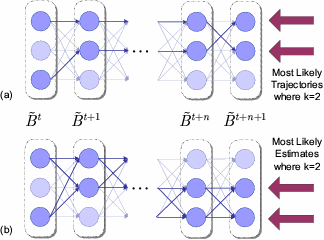
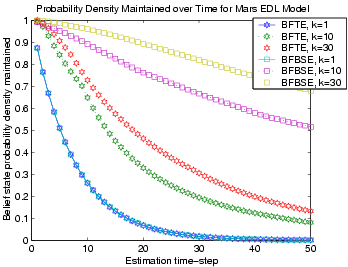
Previous work in model-based monitoring and fault diagnosis, including GDE/Sherlock [1,2], GDE+ [5], Livingstone [6,4], and Titan Mode Estimation [8]; have achieved reactivity, while maintaining reliability, by framing mode estimation as a best-first shortest-path problem, enumerating estimates in order of likelihood using a variant of the Viterbi algorithm. This approach is known as Best-First Trajectory Enumeration (BFTE), shown in Figure 1a, and works well when determining the "most likely explanation" to a sequence of observations. Unfortunately, approximating the current state by the most likely trajectory can significantly underestimate the true state probability and result in misdiagnosis. Figure 2 shows this dramatic loss in belief state probability density over time for the Mars EDL model, where the BFTE results are depicted with hexagon marks.
|
|
|
|---|---|---|
| Figure 1. Trellis Diagram of (a) BFTE and (b) BFBSE. | Figure 2. Probability density maintained over time. |
Innovation
This research introduces a novel mode estimation technique, called Best-First Belief State Enumeration (BFBSE), that approximates the belief state by generating the set of most likely estimates and achieves greater accuracy by computing the estimate probabilities directly from the Hidden Markov Model (HMM) Belief State Update equations (illustrated in Figure 1b) instead of approximating them by their trajectory probability. This contribution significantly increases the accuracy of the estimator as seen by the square marks in Figure 2.
Performance Results
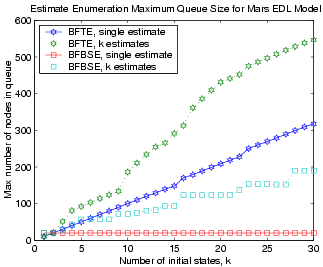
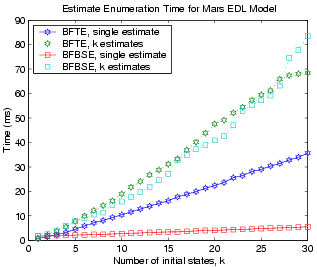
Both BFTE and BFBSE efficiently enumerate the most likely states in best-first order by framing mode estimation as an Optimal Constraint Satisfaction Problem (OCSP) and solving it using Conflict-directed A* [7]. The computational difference between these two algorithms reside in the heuristic function, where BFTE enumerates states in terms of trajectory probability and BFBSE uses the HMM Belief State Update equations. Although BFBSE incurs additional arithmetic computations, the runtime (Figure 3) is relatively unaffected for moderate sized models and requires less memory (Figure 4) when tracking more than a couple states (k > 2).
|
|
|
|---|---|---|
| Figure 3. Maximum queue size for BFTE and BFBSE. | Figure 4. Time required for BFTE and BFBSE. |
Future Work
Although BFBSE has been shown to increase estimator accuracy while using less memory and, under certain conditions, less computational time; further improvements to BFBSE should result from our current work to correctly update the prior state probabilities with a valid observation probability distribution. Efficient use of the observation probabilities in the OCSP objective function should also lead to better diagnostic discrimination, pruning lower probability states earlier in the search.
Research Support
This research was funded in part by the Jet Propulsion Laboratory, through the JPL Director’s Research and Development Fund.
References:
[1] J. de Kleer and B. C. Williams. Diagnosing multiple faults. Artificial Intelligence, 32(1):97--130, 1987.
[2] J. de Kleer and B. C. Williams. Diagnosis with behavioral modes. In Proceedings of IJCAI-89, pages 1324--1330, 1989.
[3] M. Ingham. Timed Model-based Programming: Executable Specifications for Robust Mission-Critical Sequences. PhD thesis, MIT, Department of Aeronautics and Astronautics, Cambridge, MA, 2003.
[4] J. Kurien and P. Nayak. Back to the future for consistency-based trajectory tracking. In Proceedings of AAAI-00, pages 370--377, 2000.
[5] P. Struss and O. Dressler. "Physical Negation" - Integrating fault models into the General Diagnostic Engine. In Proceedings of IJCAI-89, pages 1318--1323, 1989.
[6] B. C. Williams and P. Nayak. A model-based approach to reactive self-configuring systems. In Proceedings of AAAI-96, volume 2, pages 971--978, Portland, OR, August 4-8, 1996.
[7] B. C. Williams and R. Ragno. Conflict-directed A* and its role in model-based embedded systems. Accepted for publication in the Journal of Discrete Applied Math, 2005.
[8] B. C. Williams, M. D. Ingham, S. H. Chung, and P. H. Elliott. Model-based programming of intelligent embedded systems and robotic space explorers. In Proceedings of the IEEE, 91(1):212--237, January 2003.
The Stata Center, Building 32 - 32 Vassar Street - Cambridge, MA 02139 - USA tel:+1-617-253-0073 - publications@csail.mit.edu (Note: On July 1, 2003, the AI Lab and LCS merged to form CSAIL.) |
