Research Abstracts - 2006

Inertial and Visual Constraints for 6-DOF Pose Graphs

David D. Diel & John J. Leonard

Introduction

A common problem in the field of robotics is to acquire geometric information about a robot and its environment. This task is broadly referred to as SLAM (Simultaneous Localization and Mapping), but it can be broken down into at least two sub-tasks; adding elements to a machine-friendly representation of the world, and displaying a human-friendly visualization. We will focus on map representation, leaving visualization to our neighbours in computer graphics.

Much of the prior work on SLAM applies only to specific robot configurations, sensors, and environments. It is tempting to recreate scenarios that have generated impressive results in the past. Yet, modern applications demand more generality. Therefore, we state our long-term objective as follows:

We intend to generalize the concept of adding sensed elements to an internal map representation while limiting the computational cost incurred per element and maintaining dynamic stability of the map.

In the short-term, we are setting up a tabletop environment in which several localization and/or mapping algorithms can be tested. The hardware initially will include a laptop, a fisheye camera, an inertial sensor, and a track or gantry on which the sensor package can move. We will assume that the camera optics and the inertial sensor are calibrated in some sense. The track or gantry will provide the ground truth path that will be used as a reference to evaluate the estimates that are produced by the algorithms.

Pose Graphs

The first algorithm that we will demonstrate and generalize is Olson's Fast Iterative Optimization of Pose Graphs with Poor Initial Estimates [1]. In a pose graph, nodes are created at equal intervals in time to represent the path of the robot. Links between nodes are formed by a combination of sensor data and the transformation equations that constrain the positions of the nodes. The links, or constraints, can be incremental (from one node to the next) or can span across several nodes (often called loop closing). Each constraint acts as a nonlinear spring, and all of the constraints together pull the graph into place.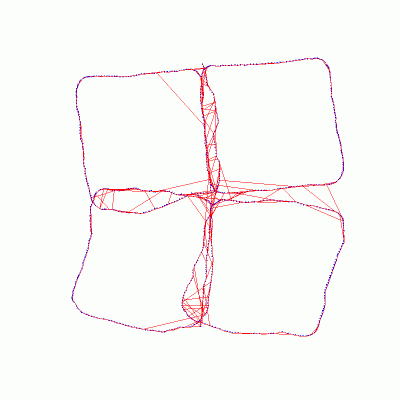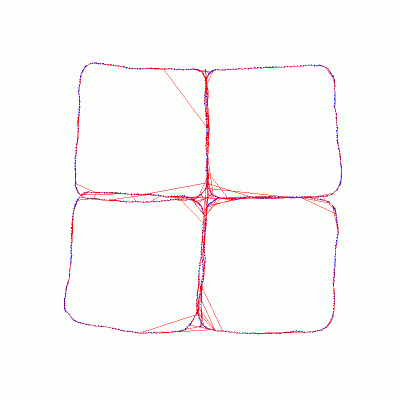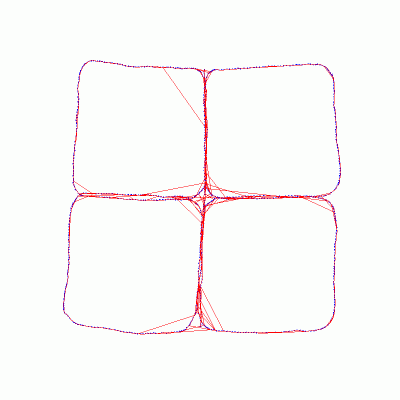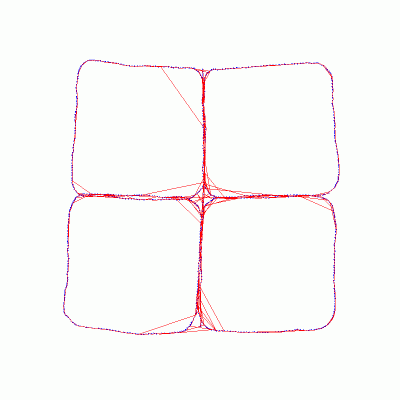

The original pose graph algorithm was formulated for 3-DOF motion only (x,y,θ), but in general, rigid bodies are free to move in 6-DOF. Furthermore, the original algorithm assumed full-rank constraints (Δx,Δy,Δθ), but sensors in general may provide anywhere from 1/2-DOF to 6-DOF information. Therefore, we are currently rewriting the algorithm in 6-DOF and deriving equations for partial constraints.

There are similarities between the pose graph formulation and the finite element method typically used to calculate stresses in mechanical parts. The map is like a physical object made of flexible material; the nodes are nodes and the constraints are like finite elements. It may be possible to use existing finite element code as the central engine for SLAM, replacing pose graphs, but there are many details to be worked out.

Constraints and Sensors

In practice, pose graph constraints have been formulated for odometry and laser scan data, but the concept should be general enough to apply to other sensors. We want to test this generalization in our tabletop environment, given inertial and visual data.

Inertial data refers to angular rates and accelerations measured in a body frame. Angular rates are similar to rotational odometry, so the analogy between them will be direct. But, acceleration does not so easily fit into the constraint framework. When a constraint is applied to a pose graph, every node within the span of the constraint is adjusted in one way, and every node beyond the span is adjusted in a different way. The adjustment equations for odometry-like measurements are known, but different adjustment equations for acceleration-like measurements still need to be derived.

Finally, we plan to incorporate our prior work on visual epipolar constraints [2]. The vision system will track point features and acquire partial constraints that span as many nodes as possible. If the body moves enough, and enough features are tracked, then the cumulative effect of the partial constraints will be to fully constrain each pose with respect to several other poses.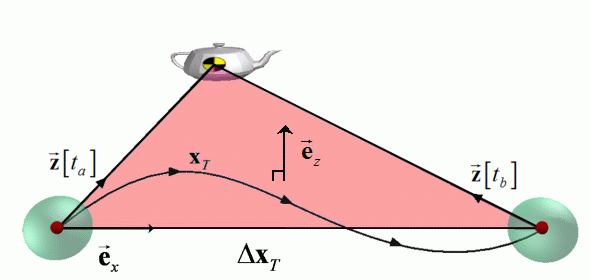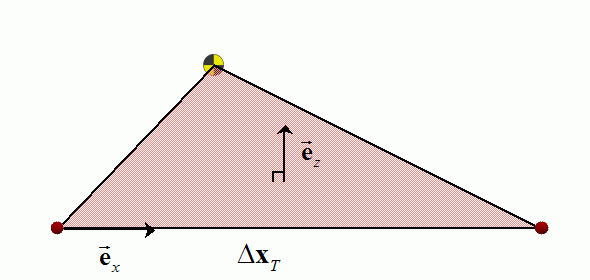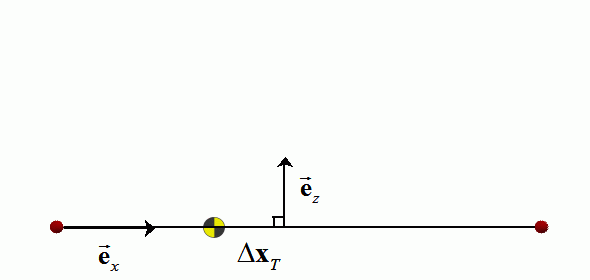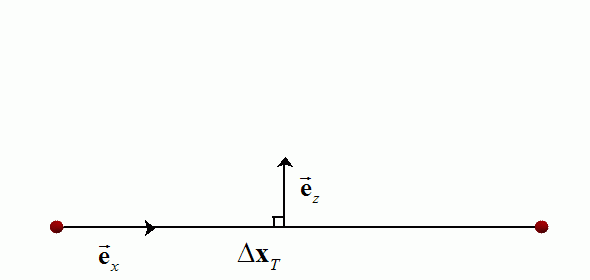

Research Support

This material is based upon work supported by Draper Laboratory, the Air Force Research Laboratory (AFRL) under Contract No. F33615-98-C-1201, and NASA under Grant No. NNA04CK91A. Any opinions, findings, conclusions, or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the sponsors.

References:

[1] Edwin Olson, John Leonard, and Seth Teller. Fast Iterative Optimization of Pose Graphs with Poor Initial Estimates. In Proceedings of the International Conference on Robotics and Automation, 2006.

[2] David Diel, Paul DeBitetto, and Seth Teller. Epipolar Constraints for Vision-Aided Inertial Navigation. IEEE Motion and Video Computing, pp. 221--228, Breckenridge, CO, USA, January, 2005.