Research Abstracts - 2006

Optimal Temporal Planning at Reactive Time Scales via Dynamic Backtracking Branch-and-Bound

Robert T. Effinger & Brian C. Williams

Abstract

In dynamic environments, autonomous robots face a host of new challenges such as: timing perturbations, component failures, and varying performance due to environmental conditions. This project proposes a closed-loop planner which continually monitors, understands, and adapts to its environment, in order to optimally achieve high-level goals. The planner is able to quickly eliminate infeasible and suboptimal candidate plans via a conflict-directed branch-and-bound search algorithm.

Introduction

As Artificial Intelligence methods steadily mature, and processing speed continues to double each year, autonomous robots are being considered for increasingly capable roles in our society. Two such examples are the automation of army convoys [1] and lunar habitat construction [4]. Traditionally, autonomous robots have operated only in structured environments where changes are strictly regulated. This is no longer the case, however, in harsh and unstructured environments such as the battlefield or on the surface of the moon. In these dynamic environments, autonomous robots face a host of new challenges, such as:

• timing uncertainties and perturbations
• component/subsystem degradation and failure, and
• varying performance due to a changing environment

To operate reliably in the face of such challenges, an autonomous robot must be capable of adapting to them on a reactive time scale. We quantify an autonomous robot's reaction time with two metrics:

Average Response Time - The first metric, average response time, specifies how quickly a robot reacts on average to an unexpected change to itself or the environment.

Worst Case Response Time - The second metric, worst case response time, tells an engineer the longest time the robot will sit and think before reacting to a change to itself or the environment.

Both of these quantitative metrics are important to assess a robot’s ability to adapt on a reactive time scale to unexpected changes in the environment. Ideally, a robot’s average response time should be as fast as possible so that it can deal with changes in any environment. In addition, for a robot to be highly reliable, its worst case response time should be as close as possible to its average response time. Otherwise, the robot’s response time will be unpredictable as changes occur in the environment.

Prior Work

The Model-based Embedded and Robotic Systems Group at MIT has designed a Reactive Temporal Planner, called Kirk [2,3,5], which allows an autonomous robot to operate reliably in a dynamic environment that contains all of the challenges listed in the introduction. Kirk is based on a novel concept called model-based programming, which allows an autonomous robot to reason at a common-sense level about its own capabilities, and the world around it, through simple, abstract models of its own capabilities, its high-level goals, and also its environment. With this knowledge, the robot can autonomously decide how to best accomplish its high-level goals, while also reasoning about its own capabilities and its environment. A diagram of Kirk’s architecture is shown in Figure 1.

Figure 1: Kirk - The Reactive Temporal Planner

Kirk requires three inputs: a high-level goal specification, a model of the robot’s capabilities, and a model of the environment. Given these inputs, Kirk will determine the optimal plan to accomplish all high-level goals, while taking into account the robot’s capabilities and its environment. Kirk is comprised of three key capabilities: a temporally-flexible plan specification, redundant and optimal method selection, and method deprecation and regeneration [2]. Each of these capabilities is designed to specifically combat one of the key challenges listed in the introduction. A brief summary of each capability is provided below.

Temporally-Flexible Plan Specification – To be robust to timing uncertainties and perturbations, Kirk uses a temporally-flexible plan specification, called a Temporal Plan Network (TPN). [5] A TPN allows flexible time-windows on the completion of activities instead of rigid timestamps. This temporal flexibility gives Kirk the ability to adjust its activity durations at run-time in response to timing uncertainties and perturbations.

Redundant and Optimal Method Selection – To be robust to component degradation and failure, Kirk allows the user to specify multiple redundant methods for accomplishing a goal. This capability allows Kirk to swap methods at run-time in response to component failures. In addition, Kirk allows the user to specify preferences between the redundant methods. This capability allows Kirk to monitor the robot’s health and performance at-run time and swap methods as necessary to ensure that the method currently in use is always the optimal one.

Method Deprecation and Regeneration – To be robust to changes in the robot’s capabilities and performance due to environmental conditions, Kirk requires an input model of the robot’s capabilities, which also specifies how those capabilities are affected by the environment. This gives Kirk the capability to react at run-time to any environmental changes that may degrade the robot’s capabilities or performance.

Problem Statement

While Kirk’s architecture is impressive in that it gives an autonomous robot the capability to operate reliably in a dynamic environment, its implementation is currently incomplete. Kirk currently runs open loop, which means that it must construct a completely new plan every time a change is detected in the environment. Kirk’s incomplete feedback loop is depicted in Figure 1 with dashed arrows.

Additionally, Kirk’s algorithmic performance in terms of response time begs improvement. The average case response time of Kirk is satisfactory on small problems but does not scale well to larger problems, and Kirk’s worst-case response time can be over 200 times worse than its average case response time even on small problems.

Project Contributions

This section is broken up into two categories, completed project contributions, and proposed (but not completed) contributions.

Completed Project Contributions

Several algorithms have been developed which improve Kirk’s average-case response time by over a factor of 10 [3], as shown in Figure 2, and improve the worst case response time by over a factor of 100. These algorithms build upon the ideas of conflict-directed search, branch-and-bound search, and heuristic search, which reason on the structure of the problem to guide the planner towards an optimal and consistent solution.

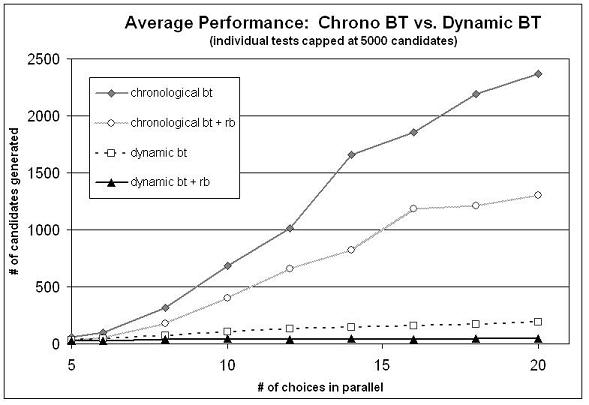Figure 2: Average Case Performance Improvements

Proposed (but not completed) Contributions

In addition, this project proposes to close Kirk’s planning loop, by augmenting the planner to continually monitor changes to the robot’s capabilities, performance, and environment, and to adjust the plan as necessary to ensure that it always optimally achieves all of its high-level goals. To accomplish this, we must complete three research tasks:

1. determine an efficient and incremental method to update the plan with new environmental information
2. test the current plan for consistency with the new info
3. find a new consistent plan if the updated information invalidates the old plan

Acknowlegements

This research is supported by NASA and DARPA.

References:

Ambrose, R., Culbert, C., and Rehnmark, “An experimental investigation of dexterous robots using EVA tools and Interfaces", In AIAA Space 2001, Albequerqe, NM.

Fredrickson, S.E., Lockhart, P.S., and Wagenknecht, J.D. “Autonomous extravehicular robotic camera (AERCam) for remote viewing. In AIAA ISS-SVC 1999, Houston, TX

Gelle, E. and Sabin M., 2003. Solving Methods for Conditional Constraint Satisfaction. In IJCAI-2003.

Ginsberg, M.L., 1993. Dynamic backtracking. In Journal of AI Research, 1:25-46.

Kim, P.; Williams, B.; and Abrahmson, M, 2001. Executing Reactive, Model-based Programs through Graph-based Temporal Planning. In IJCAI-2001.

Muscettola N., et al., 1998. Issues in temporal reasoning for autonomous control systems. In Autonomous Agents 1998.

Prosser, P., 1993. Hybrid algorithms for the constraint satisfaction problem, In Comp. Intelligence. 3, 268-299.

Shu, I., Effinger, R., and Williams, B., 2005. Enabling Fast Flexible Planning through Incremental Temporal Reasoning with Conflict Extraction. In ICAPS05 .

Rabideau, G., et.al., 1999. Iterative Repair Planning for Spacecraft Operations in the ASPEN System. In ISAIRAS 1999 .

Robertson P., et. al., “Autonomous Robust Execution of Complex Robotic Missions.” IAS, Tokyo, Japan, March 2006.

Stanford Racing Team, “Stanford Racing Team’s Entry In The 2005 Darpa Grand Challenge.” DARPA 2005 Grand Challenge Team Technical Papers.

Williams, et. al., “Model-based Reactive Programming of Cooperative Vehicles for Mars Exploration.” iSAIRAS, St-Hubert, Canada, June 2001.