CSAIL Publications and Digital Archive header
bullet Technical Reports bullet Work Products bullet Research Abstracts bullet Historical Collections bullet

link to publications.csail.mit.edu link to www.csail.mit.edu horizontal line
 

Research Abstracts - 2006
horizontal line

horizontal line

bullet Introduction

horizontal line

bullet Language, Learning, Vision & Graphics

horizontal line

bullet Physical, Biological & Social Systems

horizontal line

bullet Systems

horizontal line

bullet Theory

horizontal line

 vertical line
vertical line

On the Adaptive Real-Time Detection of Fast-Propagating Network Worms

Jaeyeon Jung, Rodolfo A. Milito & Vern Paxson

Introduction

If a network worm penetrates a site's perimeter, it can quickly spread to other vulnerable hosts inside the site. The infection propagates by the compromised host repeatedly attempting to contact and infect new potential victims. Figure 1 illustrates a situation where a firewall becomes ineffective when a user connects his infected laptop directly to the network. Hence, many networks employ a system that monitors outgoing traffic from local hosts with an attempt to quickly identify an infected host to prevent further damage.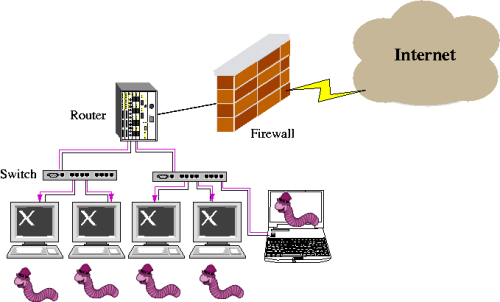

worm propagation behind a firewall

Figure 1: Peripheral defense is not enough to prevent worm propagation

The traffic pattern of fast worm propagation---a single host quickly contacting many different hosts---is a prominent feature across a number of types of worms, and detecting such patterns constitutes the basis for several worm detection approaches [1][2][3]. However, the diversity of traffic makes it difficult to tune existing worm detection methods that presume preselected thresholds for connection rates and window sizes over which to compute whether a host's activity is "too quick". Finding a single threshold rate that accommodates all (or almost all) benign hosts requires excessive tuning because of diverse application behaviors (e.g., a Web browser generating multiple concurrent connections to fetch embedded objects vs. an SSH client connecting to a server).

We develop an algorithm for detecting fast-propagating worms based on the rate at which the infected hosts initiate connections to new destinations. The foundation of our algorithm, RBS (rate-based sequential hypothesis testing), derives from the theory of sequential hypothesis testing, the use of which for detecting randomly scanning hosts was first introduced by our previous work with TRW [4]. The sequential hypothesis testing methodology enables engineering the detectors to meet false positives and false negatives targets, rather than triggering when fixed thresholds are crossed.

RBS: Rate-Based Sequential Hypothesis Testing

RBS operates on a per-host and per-connection basis and does not require access to packet contents. It is built on a probabilistic model of a typical benign host's network behavior that a benign host rarely generates more than a few first-connect connections per second, and the time intervals between those connections can be approximately modeled as exponentially distributed.

Let $ H_1$ be the hypothesis that a given host is engaged in worm propagation, and let $ H_0$ be the null hypothesis that the host exhibits benign network activity. A host generates an event when it initiates a connection to a destination with which the host has not previously communicated, i.e., when the host initiates a first-contact connection. We assume that the interarrival times of such events follow an exponential distribution with mean $ 1/\lambda_0$ (benign host) or $ 1/\lambda_1$ (scanner). When a host generates the $ i^{th}$ event at time $ t_{i}$, we can compute an interarrival time, $ X_{i} = t_{i}-t_{i-1}$ for $ i \geq 1$ and $ t_0$ the initial starting point, and update the likelihood ratio of the host being engaged in scanning (or benign).

Define $ X_1$, $ X_2$, $ \dots$, $ X_n$ as a sequence of such interarrival times. Since we model each $ X_i$ as IID negative exponential random variables, their sum, $ T_n$, is the $ n$-Erlang distribution:

$\displaystyle f_n(T_n\vert H_1) = \frac{\lambda_1(\lambda_1 T_n)^{n-1}}{(n-1)!} \exp^{-\lambda_1 T_n}$ (1)

Based on Equation (1), we can develop a sequential hypothesis test in which we define the likelihood ratio as:

$\displaystyle \Lambda(n,T_n) = \frac{f_n(T_n\vert H_1)}{f_n(T_n\vert H_0)} = \left ( \frac{\lambda_1}{\lambda_0} \right )^n \exp^{-(\lambda_1-\lambda_0)T_n}$ (2)

and the detection rules as: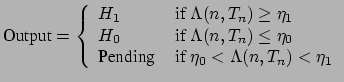

$\displaystyle \textrm{Output} = \left \{ \begin{array}{ll} {H_1} & \mbox{ if $\... ...Pending} & \mbox{ if $\eta_0 < \Lambda({n,T_n}) < \eta_1$} \end{array}\right. $

where we can set $ \eta_1$ and $ \eta_0$ in terms of a target false positive rate, $ \alpha$, and a target detection rate, $ \beta$ [5]:

$\displaystyle \eta_1$ $\displaystyle \leftarrow$ $\displaystyle \frac{\beta}{\alpha}$ (3)
$\displaystyle \eta_0$ $\displaystyle \leftarrow$ $\displaystyle \frac{1 - \beta}{1 - \alpha}$ (4)

Wald shows that setting thresholds as above guarantees that the resulting false positive rate is bounded by $ \frac{\alpha}{\beta}$ and the false negative rate is by $ \frac{1-\beta}{1-\alpha}$ [5]. Given that $ \beta$ is usually set to a value higher than 0.99 and $ \alpha$ to a value lower than 0.001, the margin of error becomes negligible (i.e., $ \frac{1}{\beta} \approx 1$ and $ \frac{1}{1-\alpha} \approx 1$).

There are four parameters to set in order to run RBS. First, $ \alpha$ and $ \beta$ give the false positive rate and the detection rate we want to achieve with the detection algorithm. In addition, we need priors, $ \lambda _1$ and $ \lambda_0$, as the reference fan-out rates. We base their selection on our simple models of the network behavior of scanners versus benign hosts.

Since a host's instantaneous first-contact rate can vary a great deal over time, RBS needs to estimate whether the current behavior provides evidence strong enough to choose one hypothesis against the other. For instance, if a host has initiated $ n$ first-contact connections and the elapsed time for the $ n^{th}$ connection is $ T_n$, RBS chooses $ H_1$ (scanner) only if the likelihood ratio $ \Lambda(n,T_n)$ exceeds $ \eta_1$. Using Equations (2) and (3), we can obtain a threshold on the elapsed time, $ T_{H_1}$, below which we arrive at an $ H_1$ (detection) decision:

$\displaystyle \frac{\beta}{\alpha}$ $\displaystyle \leq \Lambda(n,T_n)$    
$\displaystyle \frac{\beta}{\alpha}$ $\displaystyle \leq \left ( \frac{\lambda_1}{\lambda_0} \right )^n \exp^{-(\lambda_1-\lambda_0)T_n}$    
$\displaystyle \ln{\frac{\beta}{\alpha}}$ $\displaystyle \leq n\ln{\frac{\lambda_1}{\lambda_0}} - (\lambda_1-\lambda_0)T_n$    
$\displaystyle T_n$ $\displaystyle \leq n\frac{\ln{\frac{\lambda_1}{\lambda_0}}}{\lambda_1 - \lambda_0} - \frac{\ln{\frac{\beta}{\alpha}}}{\lambda_1-\lambda_0} = T_{H_1}$ (5)

Likewise, we can obtain a threshold elapsed time $ T_{H_0}$, above which we conclude $ H_0$ (benign host):
$\displaystyle T_{H_0}$   $\displaystyle = n\frac{\ln{\frac{\lambda_1}{\lambda_0}}}{\lambda_1 - \lambda_0} - \frac{\ln{\frac{1-\beta}{1-\alpha}}}{\lambda_1-\lambda_0}$ (6)


In general, Equation (5) provides important insights into the priors and the performance of RBS. $ T_{H_1}$ is a function of $ n$, taking a form of $ g(n) = a(n - c)$, where $ a = ({\ln{\frac{\lambda_1}{\lambda_0}}}) / {(\lambda_1-\lambda_0)}$ and $ c = ({\ln\frac{\beta}{\alpha}}) / {(\ln\frac{\lambda_1}{\lambda_0})}$:

  1. $ \alpha$ and $ \beta$ affect only $ c$, the minimum number of events required for detection. For fixed values of $ \lambda _1$ and $ \lambda_0$, lower values of $ \alpha$ or higher values of $ \beta$ (i.e., greater accuracy in our decisions) let more initial connections escape before RBS declares $ H_1$. One can shorten this initial holding period by increasing $ \alpha$ or decreasing $ \beta$. But we can only do so to a limited degree, as $ c$ needs to be greater than the size of bursty arrivals that we often observe from Web or P2P applications, in order to avoid excessive false alarms. Another different way to prevent damage from those initially allowed connection attempts is to hold them at a switch until proven innocent [2].

  2. Although we use $ \lambda _1$ to model a scanner's first-contact connection rate, RBS can detect any scanner with a rate $ {\lambda}'$ provided that:

    $\displaystyle {\lambda}' > \frac{1}{a} = \frac{\lambda_1-\lambda_0}{\ln {\lambda_1} - \ln{\lambda_0}}$ (7)

    because a host with a rate higher than $ {\lambda}'$ will eventually cross the line of $ T_{H_1}$ and thus trigger an alarm.

Finally, Equations (5) (6) show that RBS's decision is made based on two parameters -- the number of attempts, $ n$, and the elapsed time, $ T(n)$ and not the actual realization of the arrival process.

Results

Table 1 shows the simulation results of RBS for the trace data collected from Lawrence Berkeley Laboratory as we vary $ \lambda _1$ as a multiple of $ \lambda _0=3.83$ Hz. We obtained this reference value from the analysis of the trace data. With increasing $ \lambda _1$, we see that RBS's detection rate increases without incurring false positives. Hosts that RBS often fails to detect include an internal scanner that probed only 7 hosts in a 10 minute trace, and 6 iprint hosts that accessed only 10 or fewer other printers, sometimes in two separate 5-connection bursts, which thins out the source's average fan-out rate, making them difficult to detect. While this assessment is against a fairly modest amount of data, we find the results promising.


Table 1: Trace-driven simulation results of RBS varying $ \lambda _1$ when $ \lambda _0=3.83$ Hz, $ \alpha = 10^{-5}$, and $ \beta = 0.99$ : $ \overline {N}\vert H_1$ represents the average number of first-contact connections initiated by the flagged hosts until detection. The final line gives the theoretical bound on the slowest worm the scanner can detect (Equation (7)).
$ \lambda_1 =$ $ 2\lambda_0$ $ 3\lambda_0$ $ 4\lambda_0$ $ 5\lambda_0$ $ 10\lambda_0$ $ 15\lambda_0$ $ 20\lambda_0$ $ 25\lambda_0$
scanners (7) 4 5 6 6 7 7 7 7
Web crawlers (2) 2 2 2 2 2 2 2 2
WhatsUp (1) 0 1 1 1 1 1 1 1
iprint (6) 0 0 1 2 3 3 6 6
Total detection (16) 6 8 10 11 13 13 16 16
False positives 0 0 0 0 0 0 0 0
$ \overline {N}\vert H_1$ 30.2 18.1 13.8 10.4 6.6 5.7 5.2 5.0
Theoretical bound (Hz) $ >5.5$ $ >7.0$ $ >8.3$ $ >9.5$ $ >15.0$ $ >19.8$ $ >24.3$ $ >28.5$


This evaluation result shows that when the factor of speed difference, $ n$, between a scanner and a benign host is small, RBS requires more empirical data to arrive at a detection decision; for example, it requires on average 10.4 first-contact connections when $ n=5$, but the theoretical bound shows that it can detect any scanners that sustain more than 9.5 first-contact connections per second. In addition, as $ n$ grows larger RBS provides accurate and quick detection.

Conclusion

While built using a model that the time between connection attempts to new destinations is exponentially distributed (which we show is a reasonable approximation for bursts of activity), RBS decisions reflect the aggregate measurement of the total elapsed time over a number of attempts, not the characteristics of individual arrivals. We define RBS in terms of a single discriminating metric--the rate of connection attempts--which differs substantially between benign hosts and an important class of worms. While the choice of such a metric evokes the measurement of an average rate over a window of certain size (and the comparison of the measured rate to a fixed threshold), RBS is more elaborate. The algorithm draws from sequential hypothesis testing the ability to adapt its decision-making in response to the available measurements in order to meet specified error requirements. We can view this as an adaptation of both the window size (i.e., how many attempts to make a decision) and the threshold (i.e., what is the minimum measured rate over that window that leads to a trigger). This adaptation gives RBS a robustness unseen in fixed window/threshold schemes.

Research Support

We gratefully acknowledge funding from the National Science Foundation under Cooperative Agreement No. ANI-0225660 and Electronics & Telecommunications Research Institute, Korea.

References

[1] Jamie Twycross and Matthew M. Williamson. Implementing and Testing a Virus Throttle. In Proceedings of the 12th USENIX Security Symposium, August 2003.

[2] Stuart E. Schechter, Jaeyeon Jung and Arthur W. Berger. Fast Detection of Scanning Worm Infections In Proceedings of the 7th International Symposium on Recent Advances in Intrusion Detection (RAID'04), September 2004.

[3] Shigang Chen and Yong Tang. Slowing Down Internet Worms. In Proceedings of the 24th International Conference on Distributed Computing Systems (ICDCS'04), March 2004.

[4] Jaeyeon Jung, Vern Paxson, Arthur W. Berger and Hari Balakrishnan. Fast Portscan Detection Using Sequential Hypothesis Testing. In Proceedings of the IEEE Symposium on Security and Privacy, May 2004.

[5] Abraham Wald. Sequential Analysis. J. Wiley & Sons, New York, 1947.

 

 

 vertical line
vertical line
 
horizontal line

MIT logo Computer Science and Artificial Intelligence Laboratory (CSAIL)
The Stata Center, Building 32 - 32 Vassar Street - Cambridge, MA 02139 - USA
tel:+1-617-253-0073 - publications@csail.mit.edu