Research Abstracts - 2006

LittleDog Learning Locomotion Project

A.Shkolnik, E.Brunskill, K.Rohanimanesh, M.Price, M.Walter, K. Byl, N.Roy & R.Tedrake

Introduction

The LittleDog Learning Locomotion project seeks to develop a robust control strategy to enable a quadruped robot to traverse rough terrain. Our approach utilizes a hierarchical control architecture and applies reinforcement learning techniques to produce good performance at each level of hierarchy.

Motivation

A robust walking robot that can learn and adapt to a wide variety of terrain has a large range of important applications, from search and rescue operations to exploration. In addition, the techniques used to accomplish robust walking could provide significant insight into the development of better prosthetics. Yet despite decades of effort, achieving agile robot locomotion over rough terrain remains a challenging problem. Humans easily traverse stairs and other discontinuous / rough terrains which would be prohibitive for wheeled robotics. Intuitively, one would expect legged robots to be able to achieve human or animal like performance. Why then has this not yet been achieved?

Walking turns out to be a challenging problem because the system is under-actuated. There is limited or no actuation between each foot and the ground, unlike robotic arm manipulators where the base of the system is rigidly attached to some immobile or heavy base, and an actuator at this base (and any other joints) allows for arbitrary trajectories of the end-effector to be achieved. In walking robots (or animals), if there is limited or no actuation between the base and the feet -- for example during heel-strike, toe-off, or running -- then arbitrary trajectories of the center of body can not be attained. The question is how to execute the task of walking (moving the center-of-body forward) as closely as possible, while avoiding catastrophic areas of the state space, in which falling becomes inevitable. Conventional control methods simply do not work under such a regime.

In addition, while it is critical for the robot to maintain stability throughout the walking process, the two most popular stability functions used in robotics are overly conservative. Both the static stability margin and the zero moment point (ZMP) methods involve ensuring that the center of mass (or pressure) lies inside a support polygon defined by the other limbs. However, for animals and humans, these criteria are frequently violated: strobe images of running reveal a part of the stride where all feet are off the ground, a stable configuration that is clearly violating both of the above measures of stability. We also seek to develop a new less conservative definition of stability in order to allow the robot to move faster.

Approach

In order to develop a robust control strategy to enable a quadruped robot to traverse rough terrain we organized the task into a hierarchy. At the highest level, a foot planner selects the best next foot position for the swinging foot to land. Given this desired location, the foot trajectory generator determines a velocity profile (trajectory) for the stepping foot to follow as it lifts off the ground, swings through the air, and touches down to the ground in the specified location. Finally, a lower level joint controller performs inverse kinematics, and converts foot trajectories from the swing foot trajectory generator into joint position and velocity commands.

Foot Placement Planner

The foot placement planner selects the next positions for the feet. It is assumed that the robot is given a goal location to reach. Currently, next foot positions are sampled from a Gaussian distribution around a step of fixed size directly towards the goal. A cost is then computed for each potential sample: the cost of a step includes its potential stability (the probability that if the robot executed that step that it would fall), and the distance it advances the robot towards the goal location. The sample with the lowest cost is selected and passed on to the foot trajectory generator. We are currently employing a heuristic stability measure to evaluate potential samples. We plan to learn the stability function through experience, and use this to learn the parameters of a generative function. Furthermore, we intend to use this generative function to produce potential sample next foot positions. A generative function will reduce the computational cost of the foot planner, and will also allow the foot planner to do efficient multi-step planning.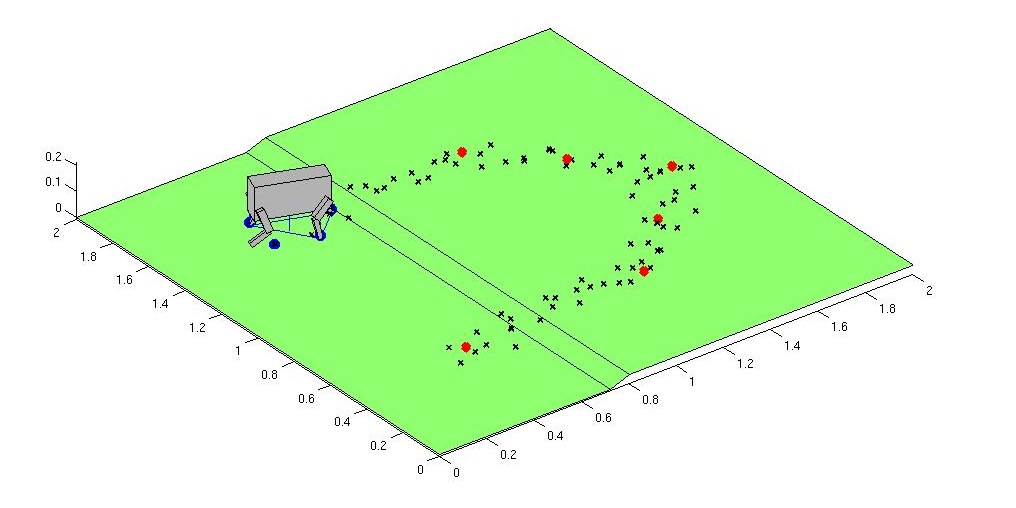

Foot Trajectory Planner

A finite state machine is utilized to characterize each foot as being in one of four states: stance, lift, swing or down. During lift / swing / down phases, a trajectory for the foot is to be generated to bring the foot from its current position to a position which is as close as possible to the desired foot position, as provided by the foot planner. An infinite set of trajectories exist to satisfy this task; one will be selected to satisfy some optimization criteria, for example jerk (the third derivative of position). Machine learning techniques will be further applied to select trajectories which enhance the stability and robustness of execution during each step.

Joint Controller

The position / velocity of feet in the air, as specified by the state machine, must be converted to joint angle velocities of the body and legs. There are typically an infinite number of solutions to this inverse kinematics problem. The joint controller is responsible for resolving redundancies between links, given that multiple feet will be on the ground at the same time, in order to prevent internal forces from pushing and tugging on the center of body in different directions by separate legs. The joint controller must also determine joint velocity trajectories which maximize stability. In order to create a robust joint-controller, we compute the whole body Jacobian and select points inside the Jacobian

Preliminary Results

We have currently implemented a Matlab simulation of the little dog robot which includes the foot placement planner, the foot trajectory planner and joint controller. The simulator allows us to explore different terrain, and the simulated robot has successfully walked and navigated simple steps.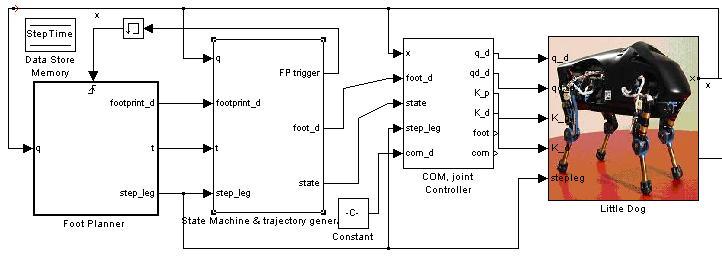

Future Work

This project is still in its initial stages. We later intend to incorporate more learning into all three levels of the hierarchy. We also expect that experiments conducted on the real quadruped robot that we recently acquired for this project will also lead to further modifications to our approach.

Research Support

This project is supported by DARPA IPTO through the Learning Locomotion program.