Research Abstracts - 2006

DNA-Protein Binding and Games

L. Pérez-Breva, L. E. Ortiz, C-H. Yeang¹ & T. Jaakkola

The Problem

We propose a game-theoretic approach to learn and predict coordinate binding of multiple DNA binding regulators. The binding game implements resource constrained allocation of proteins to local neighborhoods and to sites themselves, and explicates coordinate and competitive binding relations among proteins with affinity to the site or region.

Our initial work [9] focused on mathematical foundations of the new modeling approach, and illustration in the context of a well known biological sybsystem. We showed that every binding game has an equilibrium and that one can be found efficiently. We provided simulation results on the lambda-phage switch that successfully illustrate the predictions that can be derived from the model with known structure and affinities.

Our current work elaborates on methods for learning the affinities and game structures from available binding data.

Motivation

Effective transcriptional control relies in part on coordinate operation of DNA binding regulators and their interactions with various co-factors. Understanding such processes is challenging, however, since the role of interactions or binding sites associated with any specific genes may not be transparent if considered in isolation.

We believe game theory and economic models provide an appropriate framework for understanding (and searching for) the context and constraints associated with interacting regulatory processes. Resource constraints, for example, are critical to understanding who binds where. Overlapping or close binding sites create explicit competition for the sites. Similarly, explicit coordination — formation of larger protein complexes — may be required for binding or, alternatively, binding may be facilitated by the presence of another protein. Most importantly, game theory, by its very nature, provides meaningful (causal) predictions under substantial perturbations of individual "players." Previous work in game theory and economics (see [8] and [2] for classical examples, and [5] for a thorough introduction,) provides a solid mathematical foundation for our modeling approach.

Our approach deviates from an already substantial body of computational methods used for resolving transcriptional regulation. Much of the recent work has been statistical in nature as in identifying regulatory modules either by combining available binding data with mRNA expression profiles [3] or by relating mRNA levels of candidate regulators directly to their potential targets [13]. Our work is closest in spirit to more detailed reaction equation models [7, 1], while narrower in scope due to our preliminary focus on binding alone. Our conceptualization of the binding problem is nevertheless different, and the mathematical modeling approach is clearly distinct from reaction equation models, even in terms of the level of analysis.

Approach

To formalize the game we further decompose the binding problem into transport and local binding. By transport, we refer to the mechanism that transports proteins to the neighborhood of sites to which they have affinity. The biological processes underlying the transport are not well-understood although several hypotheses exist[15, 4]. We abstract the process by assuming separate affinities for proteins to explore neighborhoods of specific sites, modulated by sites availability.

Local binding, on the other hand, captures which proteins bind to each site as a consequence of local accumulations or concentrations around the site. Assuming that each site's neighborhood constitutes a chemically well-mixed and closed system, we model binding as being governed by chemical equilibria.

Broadly speaking, transport and local binding yield an arrangement of proteins along the possible DNA binding sites. This is what we aim to predict with our game-theoretic models. These arrangements are in principle observable from binding assays (cf. [12]). Nevertheless, the predictions of our model can be viewed as functions of the overall (nuclear) concentrations of proteins, the affinities of proteins to explore neighborhoods of individual sites, as well as the equilibrium constants characterizing the ability of proteins to bind to specific sites when in close proximity. Any perturbation of such parameters leads to a potentially different arrangement that we can predict. The game provides the mechanisms for arriving at such predictions.

We abstract the notion of proteins and DNA binding sites by viewing them as rational agents or players competing non-cooperatively in a game. The binding game has no global objective function that guides the players choice of strategy. The players choices are instead guided by their own utilities that depend on the choices of other players. We assume that the biological system being modeled reaches a steady state, at least momentarily, preserving the average allocations. The predictions we can make based on the game-theoretic formulation are equilibria of the game and correspond to these steady states.

Preliminary Work

We have shown that protein-DNA binding game has an equilibrium. We emphasize that there is no reason a priori to believe that there exists an equilibrium in the pure strategies. The existence is guaranteed by the following theorem:

Theorem 1. Every protein-DNA binding game has an equilibrium.

The proof can be obtained either through Brower's fixed point theorem or, alternatively, on the basis of the algorithm we have developed for finding equilibria of the game. The theorem guarantees that at least one equilibrium exists but there may be more than one.

The equilibria of the binding game represent predicted binding arrangements. It is therefore critical to be able to find equilibria on a genome-wide scale. While finding Nash equilibria of multi-person games is known to be hard, we exploit the simple bi-partite structure of our game (utilities of proteins only involve sites and viceversa,) to find an equilibrium efficiently through a simple iterative al- gorithm. The algorithm monotonically fills the sites up to the equilibrium levels, starting with all sites empty. The algorithm is guaranteed to converge to a solution of the game.

We tested our model empirically on the lysogeny state of lambda-phage infection [6, 14, 1]. Our results show that the predictions of our model are consistent with what is known about the lysogeny state. The lysogeny game has two protein-players, RNA-polymerase and cI₂ , and three site-players, OR1, OR2, and OR3, and in our simulations, we set the game parameters in accordance with the chemical properties reported in previous work [14, 10, 11]. As an illustration. the Figure below captures the change in probability of binding at different sites as a function of increasing availability of cI₂ . Although our model does not capture dynamics the figure is nonetheless useful for assessing quantitative changes and the order of events as a function of increasing cI₂ . Note, for example, that the levels at which cI₂ occupies OR1 and OR2 rise much faster than at OR3. While the result is expected, the behavior is attributed to protein-protein interactions which are not encoded in our model. The figure suggests that cooperative binding can also be obtained as a by-product of competition involving RNA-polymerase, cI₂, OR1, and OR3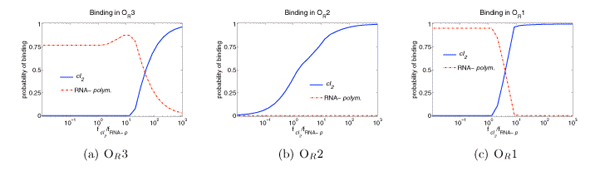

Discussion and Ongoing Work

We believe the game-theoretic approach provides a compelling causal abstraction of biological systems with resource constraints. The model is complete with provably convergent algorithms for finding equilibria on a genome-widescale.

The results from the small scale application are encouraging. Our model successfully reproduces known behavior of the lambda−switch on the basis of molecular level competition and resource constraints, without the need to assume protein-protein interactions between cI₂ dimers and cI₂ and RNA-polymerase. Even in the context of this well-known sub-system, however, few quantitative experimental results are available about binding. Proper validation and use of our model therefore relies on estimating the game parameters from available protein-DNA binding data (in progress). Once the game parameters are known, the model provides valid predictions for a number of possible perturbations to the system, including changing nuclear concentrations and knock-outs.

Research Support

This work is supported in part by NIH grant GM68762 and by NSF ITR grant 0428715. Luis Perez-Breva is a fellow from Fundación Rafael del Pino.

References:

[1] Adam Arkin, John Ross, and Harley H. McAdams. Stochastic kinetic analysis of developmental pathway bifurcation in phage lambda-infected escherichia coli cells. Genetics, 149:1633-1648, August 1998.

[2] Kenneth J. Arrow and Gerard Debreu. Existence of an equilibrium for a competitive economy. Econometrica, 22(3):265-290, July 1954.

[3] Z. Bar-Joseph, G. Gerber, T. Lee, N. Rinaldi, J. Yoo, B. Gordon F. Robert, E. Fraenkel, T. Jaakkola, R. Young, and D. Gifford. Computational discovery of gene modules and regulatory networks. Nature Biotechnology, 21(11):1337-1342, 2003.

[4] Otto G. Berg, Robert B. Winter, and Peter H. von Hippel. Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. models and theory. Biochemistry, 20(24):6929-48, November 1981.

[5] Drew Fudenberg and Jean Tirole. Game Theory. The MIT Press, 1991.

[6] Ira Herskowitz and David Hagen. The lysis-lysogeny decision of phage lambda: Explicit programming and responsiveness. Annual Reviews Genetics, 14:399-345, 1980.

[7] HarleyH. McAdams and Adam Arkin. Stochastic mechanisms in geneexpression. PNAS, 94(3):814-819, 1997.

[8] John Nash. Non-cooperative games. The Annals of Mathematics, 54(2):286-295, September 1951.

[9] Luis Pérez-Breva, Luis Ortiz, Chen-Hsiang Yeang, and Tommi Jaakkola. DNA binding and games. Technical Report MIT-CSAIL-TR-2006-018, Massachusetts Institute of Technology, Computer Science and Artificial Intelligence Laboratory, March 2006.

[10] Mark Ptashne. A Genetic Switch: Gene control and phage lambda. Cell Press AND Blackwell Scientific Publications, 3rd edition, 1987.

[11] Mark Ptashne and Alexander Gann. Genes and Signals. Cold Spring Harbor Laboratory press, 1st edition, 2002.

[12] Bing Ren, Franois Robert, John J. Wyrick, Oscar Aparicio, Ezra G. Jennings, Itamar Simon, Julia Zeitlinger, Jrg Schreiber, Nancy Hannett, Elenita Kanin, Thomas L. Volkert, Christopher J. Wilson, Stephen P. Bell, , and Richard A. Young. Genome- wide location and function of DNA-binding proteins. Science, 290(2306), December 2000.

[13] E. Segal, M. Shapira, A. Regev, D. Pe'er, D. Botstein, D. Koller, and N. Friedman. Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nature Genetics, 34(2):166-76, 2003.

[14] Madeline A. Shea and Gary K. Ackers. The or control system of bacteriophage lambda. a physical-chemical model for gene regulation. Journal of Molecular Biology, 181:211- 230, 1985.

[15] Neil P. Stanford, Mark D. Szczelkun, John F. Marko, and Stephen E. Halford. One- and three-dimensional pathways for proteins to reach specific DNA sites. EMBO, 19(23):6546-6557, December 2000.

^{1 - C-H. Yeang's affiliation is with the University of California, Santa Cruz, CA}