Research Abstracts - 2006

Robust Network Connectivity: When It's The Big Picture That Matters

Enoch Peserico & Larry Rudolph

We characterize networks in which connectivity depends essentially only on the "big picture" structure of the network, and not on the inevitable "small scale noise" due to imprecisely positioned or faulty nodes or links. Crucial factors turn out to be not only the diameter and mincut of the network, but also the presence of large "holes" - holes interact with small scale noise seriously compromising the connectivity in the region surrounding them.

Connectivity = Large scale structure + Small scale noise

Connectivity between distant regions in large diameter networks depends on two main factors: large scale structure and small scale noise. The large scale structure of a network is typically linked to the topography of the area in which the network is deployed. For example, a city-wide adhoc radio network is essentially two dimensional (but could have an elongated shape in the case of a city along a river or in a narrow mountain valley) and necessarily has a large number of ``holes'' in areas, such as ponds or electromagnetically shielded buildings, that nodes cannot populate and through which information cannot flow. As another example, a SmartDust large sensor network deployed on the surface of a building, of an aircraft or of a ship to detect signs of impending structural failure has a topology essentially determined by the nature of the building - a topology that could be particularly intricate in cases such as that of the Eiffel tower. Of course, there are many examples of large scale adhoc distributed peer to peer networks whose ``large scale'' topology depends not on physical factors, but on the algorithm used to form the links.

Connectivity is also affected by a level of ``small scale noise'': in large networks a fraction of the nodes is almost inevitably faulty, the deployment process is often imprecise, and sometimes mobility can alter the position of nodes over time. The effects of this noise, even when relatively limited on short range communications, can accumulate and seriously compromise long range connectivity: if every link has a probability p of failure, then the probability that a path of h hops is entirely fault free is approximately e^-hp, which becomes vanishingly small when h is much larger than the average distance between faults, 1/p. This can make long range communication problematic in large diameter networks with even a moderate level of small scale noise, such as sensor networks, large mobile radio networks, or nanotechnological ensembles.

Most of the (vast) literature on connectivity in the presence of small scale noise studies how different types and levels of small scale noise affect networks with a single, specific large scale structure - rather than how variations in large scale structure affect connectivity in the presence of a given level or range of small scale noise.

Connectivity can be independent of small scale noise: but beware of holes!

We characterize networks whose connectivity essentially depends only on their large scale structure and is independent from small scale noise. In these ``robustly linked'' networks connectivity between regions - expressed in terms of disjoint, non-faulty paths - is always, with high probability, within a small factor of the optimal.

Informally, we show that even extremely narrow strips (of width logarithmic in their length) are sufficient to guarantee good connectivity in a network with imprecisely positioned/faulty nodes and links, provided there are not too many large "holes" in the network. Large holes require larger width, since, in the presence of small scale noise, they can effectively erode connectivity in the region surrounding them to a distance that is logarithmic in the girth (informally, the ``circumference'') of the hole, and grows with the level of small scale noise.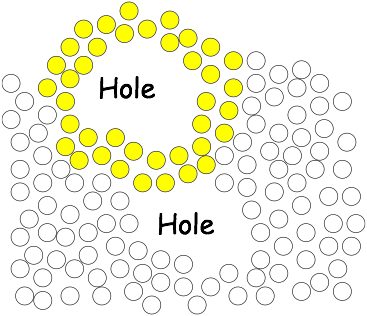

The theoretical cornerstone of our work is a formal analysis of the notion of "hole" on graphs - an intuitive notion in two dimensions, but far more subtle in higher dimensions or on general, non-planar graphs: for example, the "hole" in a doughnut is fundamentally different from that in a piece of swiss cheese. This analysis yields insights that might be of independent interest. Our theoretical analysis is validated by extensive simulations involving up to a billion nodes.

A number of consequences

Our results have a number of consequences - some of them, perhaps, surprising.

• While a truly 1-dimensional support is indeed not sufficient for a network to scalable tolerate failures, it is ``almost'' sufficient: our result shows that networks can have extremely elongated shapes (e.g. millions of nodes long and only a few dozen nodes wide - the aspect ratio of a typical fishing line!) and still tolerate well a fairly high failure rate. For the same reason, "controlled flooding" between two zones of a network can be restricted to extremely narrow strips between them.
• Considering connectivity between two zones that, in the absence of failures, are linked by a number of disjoint paths at least logarithmic in the distance between the two zones, rather than between two points that are connected by a single path, has two considerable advantages. First, it allows one to amortize the necessary logarithmic width of the connecting strip, since the two zones are connected by a logarithmic number of disjoint fault-free paths. Second, it makes the probability that there are not at least that many fault-free paths between the two zones exponentially small in the width of the strip - whereas clearly a constant failure probability is the best one can achieve when considering simple point to point connectivity.
• The presence of holes, particularly holes with a circumference much larger than the expected distance between faults, can seriously degrade the ability of a large network to maintain its connectivity in the presence of faults. Two networks that, in the absence of faults, have the same diameter and the same bandwidth, can exhibit radically different connectivity in the presence of faults if one of them contains a large number of large holes with thin ``walls'' around them. This should be kept in mind when simulating the behavior large networks in realistic environments which inevitably have large ``holes'' (bodies of water, electromagnetically shielded buildings, etc.) - restricting one's analysis to e.g. a solid disc or the unbroken surface of a sphere could lead to excessively optimistic results.
• In order to guarantee high availability of connectivity between two areas of a network, designers typically try to ensure that they are connected by a virtual network formed by multiple completely disjoint paths. This approach might be valid when the two areas are separated by a number of hops smaller than 1/p, where p is the probability of failure at any given hop - in other words, when the probability that any single path is entirely fault-free is relatively high. However, it is remarkably ineffective if the distance between the two areas is much larger than 1/p. In this case the only option to safeguard connectivity (without resorting to an exponentially large number of disjoint paths) is instead to keep the paths connecting two areas tightly linked, in such a way that one can ``splice'' together non-faulty portions of different, faulty paths to obtain a new, entirely non-faulty path.
• In a geometric radio network or in a nanotechnological ensemble, a larger number of smaller cells is desirable not only because it provides higher bandwidth in the absence of faults. In the presence of faults a larger number of smaller cells guarantees a constant fraction of that larger, ``ideal'' bandwidth with higher probability. This is a consequence of the logarithmic ratio between the width and length of a strip between regions (and around holes) that is sufficient to guarantee good connectivity. Therefore - somewhat counterintuitively - cell size reduction can produce by itself an improvement in the overall reliability of the resulting network even when not accompanied by an improvement in the reliability of the individual cells themselves.

Acknowledgments:

This work was funded in part by the Singapore-MIT-Alliance (SMA).

References:

[1] Enoch Peserico, Larry Rudolph. Robust network connectivity: when it's the big picture that matters. Proceedings of ACM SIGMETRICS 2006.