Research Abstracts - 2006

Distributed Control for Multiple Robots

Keith Kotay & Daniela Rus

Background

Our goal is to develop distributed algorithms that allow a group of robots to achieve a global task without global coordination. For small numbers of robots, a centralized control scheme is practical, but it does not scale as the numbers of robots increases. A distributed algorithm allows the robot to make control decisions based on the state of the local environment, and possibly some static global knowledge such as a desired goal shape in the case of a self-assembly task (see below). Insects are known to achieve complex assembly and foraging behaviours based on simple local rules--we would like to achieve similar, provably correct results for distributed robot algorithms.

This research began in the context of self-reconfiguring robots, which are modular robots that are physically connected and can achieve structural geometric changes autonomously [1-3]. Our approach is based on an abstract cube-shaped module with simple movement types, as shown in Fig. 1. We have developed locomotion algorithms for environments without and with obstacles (Fig. 3), as well as self-assembly algorithms for creating a goal shape in a specified location (Fig. 4) [4-7]. We are now extending this research to teams of robots that are not physically connected (Fig. 5).

Approach

Our generic distributed approach to developing algorithms for self-reconfiguring robots has previously been described in [4-7]. The goal is to develop architecture-independent self-reconfiguring algorithms that can be instantiated to many different self-reconfiguring systems. Our approach is based on four principles:

1. Work with the simplest possible abstract module, both in shape and actuation modalities.
2. Develop functional algorithms based on the abstract module.
3. Prove the correctness of the algorithms.
4. Instantiate the algorithms onto real self-reconfiguring systems.

We have chosen to use the conceptual model of cellular automata (CA), although our system deviates from the classical CA approach in several ways. The tangible contribution of cellular automata research to our work is the use of local rules to produce global behavior. Other features of traditional cellular automata, such as non-conservation of matter and the simultaneous-update evaluation model are not appropriate for self-reconfiguring systems.

Fig. 1: Basic motions for the abstract cube module (top to bottom): linear translation, convex transition, and concave transition.

Abstract module

The use of an abstract module allows us to decouple the salient features of a self-reconfiguring module from the implementation dependent features that tend to complicate algorithm design and analysis. We generally represent the module shape as a cube, although our proposed abstraction can be replaced by any geometric structure that supports the formation of lattices. The actuation modalities for the module are the basic motions needed for motion: linear translation, convex transition, and concave transition (Fig. 1).

Algorithms

Each algorithm employs a set of local rules we implement as a type of cellular automaton. Each rule requires a set of preconditions on the neighborhood of the cell and when activated, causes a change in the system state. The rules are written in the form of productions, with the precondition state on the left and the resulting state, or postcondition, on the right (Fig. 2). The postcondition is often the movement of a module, but in some cases it is only a change in the internal state in the module. Simple algorithms may not require any internal state, while more complex algorithms may have several local variables for each module. Currently, all our rulesets are created manually, but we are investigating the automatic ruleset creation.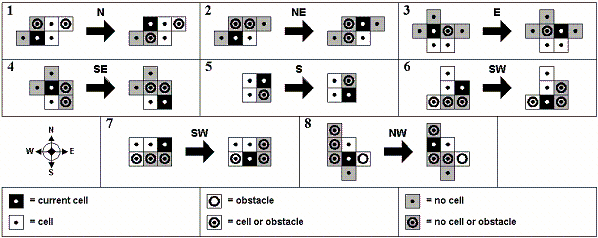

Correctness

Proof of correctness is an important principle of our approach. Our proofs take the form of logical arguments regarding the possible configurations of module groups, and of automated proofs of correctness based on an evaluation of the properties of a constructed graph representing all possible sequences of rule actuations for a given initial configuration. In this sense, an initial configuration and a rule set can be viewed as a finite automaton whose graph indicates various properties about the algorithm. We also show that simulation results can be combined with machine learning theory to produce a statistical bound on the likelihood that an algorithm is correct. This is done by performing multiple simulations using a fixed rule set and initial configuration, while evaluating modules randomly in each simulation. A specific evaluation order in which rules are executed is referred to as an activation sequence. The result of many random simulations is an exploration of the set of all possible activation sequences, which can be used to bound the expected size of the set of erroneous activation sequences.

Instantiation

Instantiation refers to the application of generic algorithms to specific hardware systems. This can be done by using meta-modules---groups of real modules which together can perform the basic motion primitives of our abstract module---or by creating "native" module motion sequences which implement the basic motions. The value of instantiation is that the proof of correctness is inherited from the abstract system, and such proofs may not exist for the system using native module motions. Refer to [6] for instantiation examples.

Algorithms

1) Locomotion: Algorithms for locomotion with and without obstacles are described in [4-6]. The cellular automata approach is well suited to locomotion algorithms, since these algorithms are not fundamentally concerned with the global shape of the robot. Thus, the shape is free to be dynamically altered at the local module level, using local rules. In fact, local conformity of the shape to unknown, rough terrain is an advantage for locomotion (Fig. 3). Locomotion algorithm extensions, such as climbing tall obstacles and moving through tunnels, are presented in [6]. A proof for the correctness of this ruleset is also given in [6].

Fig. 3: Image sequence of a self-reconfiguring robot locomotion task. The grey cubes represent obstacles and the colored cubes are the robot modules (layers in the Z dimension are colored differently). Each module evaluates the ruleset independently, executing rules when the local environment matches a rule precondition (see Fig. 2).

2) Self-assembly: Although our generic distributed approach is well-suited to locomotion tasks, we are interested in exploring whether our approach can be used for non-locomotion algorithms such as building specific shapes. Here, the algorithm must be able to control shape formation using only local rules. Our results demonstrate that it is possible to achieve global shape control using only local rules for some shapes [7].

A key component of our assembly algorithm is that modules know the goal shape, the location of goal shape, and their location. While this information is a type of global knowledge, it does not require modules to obtain global information during the reconfiguration. Modules can be provided with the goal shape and their starting location prior to the start of the reconfiguration and during the reconfiguration they only need to update their location as they move, which does not require any external information.

Fig. 4 shows a simulation of a bridge building task with 300 modules. In this case the modules know the goal shape and the build direction. The initial configuration shape is arbitrary. As modules move they check to make sure they are not exiting the goal shape if they have entered it. The ruleset consists of 66 rules. 100,000 random simulations were performed on this ruleset without error, giving an appoximately 99.99% probability with a confidence of 99.99% that the ruleset is correct [5,7]. The average number of moves required to build the bridge is approximately 9512.

Fig. 4: Self-assembly of a bridge. Grey cubes represent the foundations of the bridge on each bank. Yellow cubes are inactive, cyan cubes are moving southward, and magenta cubes are moving in a direction other than southward.

3) Follow-the-leader: The previous algorithms were developed for self-reconfiguring robots, which require the structure to remain connected at all times. This is because a single module cannot move on its own due to its limited number of degrees of freedom. We are now exploring the use of our distributed control method for teams of independent robots. Fig. 5 shows a small part of a simulation of a follow-the-leader task. The goal is for a robot team to follow a leader entity shown in red (it could be another robot or a human being). Other related work achives this task by using robot swarms which seek to surround and move with the leader. However, our motivation is a bit different: we want to limit the number of moving robots so the stationary robots can act as localization reference points for the moving robots. Also, with a sufficient number of robots it would be possible to maintain a connected network from the start point to the current position of the leader--this would be useful for maintaining a sensor network along the leader's path, perhaps to detect dangerous conditions along the route of escape. In addition, the sensor network can function as a communication resource to the outside world in situations where radio range is limited by environmental conditions.

The follow-the-leader ruleset has 174 rules, however many of the rules are duplicated for the north, east, south, and west directions; the actual number of individual rules is 52. Due to the simulated sensing and positioning errors introduced to model real robot uncertainty, this ruleset sometimes fails to produce a successful simulation. This is due to an incorrect rule activation which occurs when the robot has an inaccurate model of its local environment. In the abscence of uncertainty, no errors have been observed. Further research is in progress to reduce the effect of uncertainty on the algorithm.

Fig. 5: Follow-the-leader task. The red cube represents the leader, and the other cubes represent the followers. Green cubes have internal state which identifies them as being in the center row, while blue cubes are in an outer row. In this simulation the robots are not physically connected--they must use sensing and shared connectivity information to determine their local environment. Simulated sensing/movement error causes robots to be slightly misaligned with their neighbors.

Research Support

Support for this work was provided through NSF awards IRI-9714332, EIA-9901589, IIS-9818299, IIS-9912193 and EIA-0202789 and ONR award N00014-01-1-0675. We are grateful for this support.

References:

[1] K. Kotay, D. Rus, M. Vona, and C. McGray. The self-reconfiguring robotic Molecule: design and control algorithms, Proc. of the Workshop on the Algorithmic Foundations of Robotics, Houston, USA, 1998.

[2] K. Kotay, D. Rus, M. Vona, and C. McGray. The Self-reconfiguring Robotic Molecule, Proceedings of IEEE Intl. Conf. on Robotics and Automation, Leuven, Belgium, 1998.

[3] K. Kotay and D. Rus. Locomotion versatility through self-reconfiguration, Robotics and Autonomous Systems, vol. 26, pp. 217--232, 1999.

[4] Z. Butler, K. Kotay, D. Rus, and K. Tomita. Generic Decentralized Control for a Class of Self-Reconfigurable Robots, Proceedings of IEEE Intl. Conf. on Robotics and Automation, Washington, DC, USA, 2002.

[5] K. Kotay. Self-Reconfiguring Robots: Designs, Algorithms, and Applications, Ph.D. Thesis, Dartmouth College, Computer Science Department, 2003.

[6] Z. Butler, K. Kotay, D. Rus, and K. Tomita. Generic Decentralized Locomotion Control for Lattice-Based Self-Reconfigurable Robots, Intl. Journal of Robotics Research, vol. 23, no. 9, 2004.

[7] K. Kotay and Daniela Rus. Generic Distributed Assembly and Repair Algorithms for Self-Reconfiguring Robots, Proc. of the Intl. Conf. on Intelligent Robots and Systems, Sendai, Japan, 2004.