Research Abstracts - 2007

Summary

Mean shift is a popular method to segment images and videos [1]. Pixels are represented by feature points, and the segmentation is driven by the point density in feature space. We introduce the use of Morse theory to interpret mean shift as a topological decomposition of the feature space into density modes. This allows us to build on the watershed technique and design a new algorithm to compute mean-shift segmentations. In addition, we introduce the use of topological persistence [2] to create a segmentation hierarchy. We validated our method by clustering images using color cues. In this context, our technique runs faster than previous work, especially on videos and large images. We evaluated accuracy with a classical benchmark [3] which shows results on par with existing low-level techniques, i.e. we do not sacrifice accuracy for speed.

The following figure shows a sample result obtained with our algorithm. We obtain a hierarchical segmentation at no additional cost.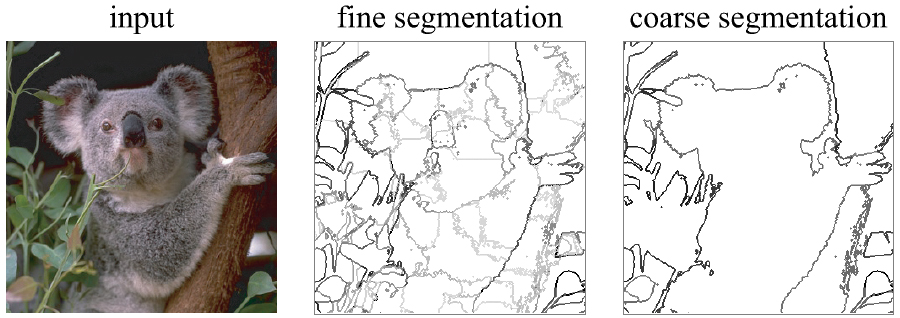

References:

[1] Dorin Comaniciu and Peter Meer. A Robust Approach toward Feature Space Analysis In IEEE Transactions on Pattern Analysis Machine Intelligence, 2002.

[2] Herbert Edelsbrunner, John Harer and Afra Zomorodian. Hierarchical Morse-Smale complexes for piecewise linear 2-manifolds. In Discrete and Computational Geometry, 2003.

[3] David Martin, Charless Fowlkes, Doron Tal and Jitendra Malik. A Database of Human Segmented Natural Images and its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics. In Proceedings of the International Conference on Computer Vision, 2001.