Research Abstracts - 2007

Summary:

Bayesian inference has become increasingly important in statistical machine learning. Exact Bayesian calculations are often not feasible in practice, however. A number of approximate Bayesian methods have been proposed to make such calculations practical, among them the variational Bayesian (VB) approach. The VB approach, while useful, can nevertheless suffer from slow convergence to the approximate solution. To address this problem, we propose Parameter-eXpanded Variational Bayesian (PX-VB) methods to speed up VB. The new algorithm is inspired by parameter-expanded expectation maximization (PX-EM) and parameterexpanded data augmentation (PX-DA). Similar to PX-EM and -DA, PX-VB expands a model with auxiliary variables to reduce the coupling between variables in the original model. We analyze the convergence rates of VB and PX-VB and demonstrate the superior convergence rates of PX-VB in variational probit regression and automatic relevance determination.

Results: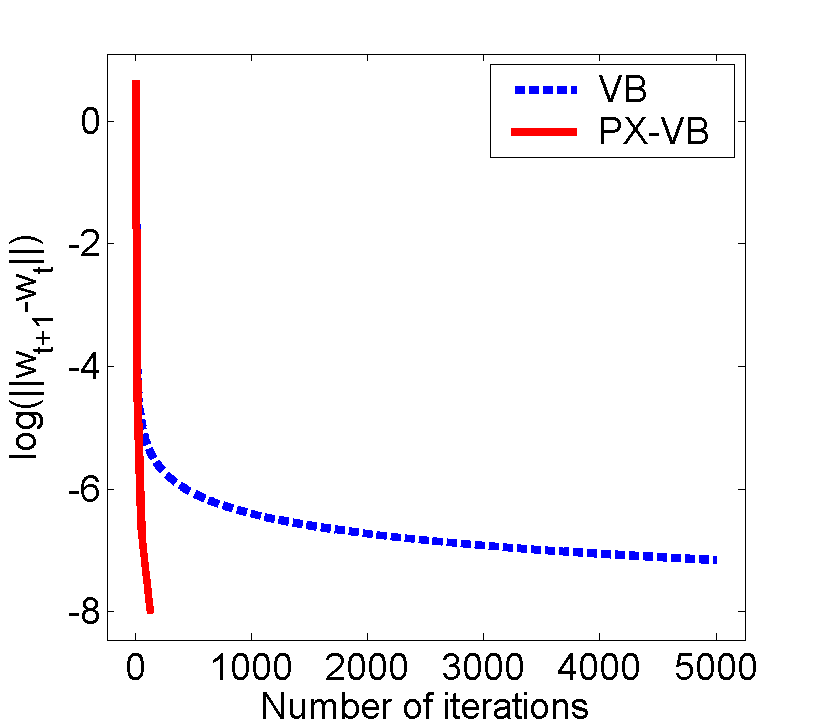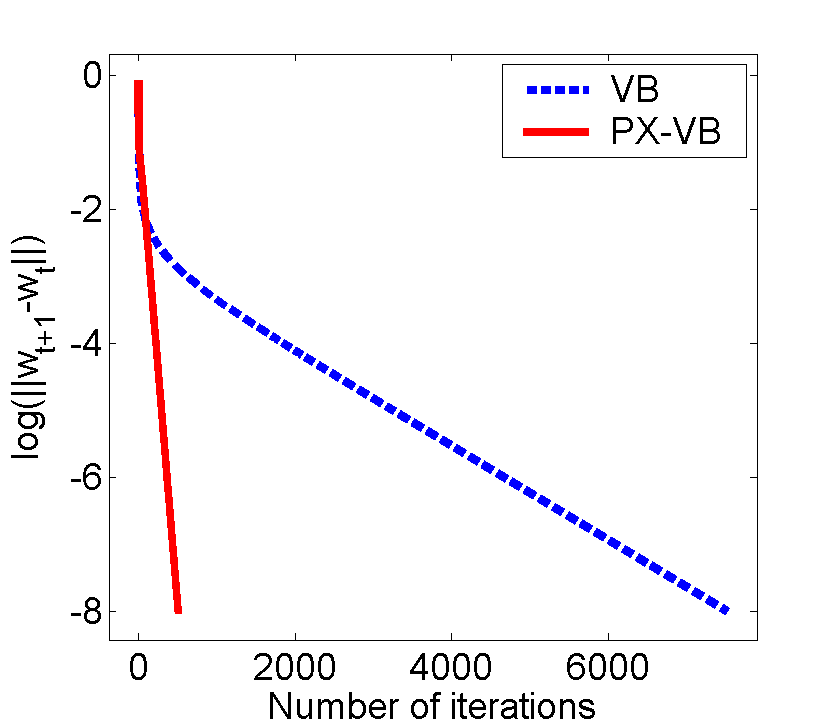

Comparison between VB and PX-VB for probit regression on synthetic (a) and kidneybiospy data sets (b). PX-VB converges significantly faster than VB. Note that the Y axis shows the difference between two consecutive estimates of the posterior mean of the parameter w.

Reference:

Parameter Expanded Variational Bayesian Methods, Y. Qi and T.S. Jaakkola, in Advances in Neural Information Processing Systems 19, MIT Press, Cambridge, MA, 2007. Link