Research Abstracts - 2007

Abstract

Reciprocity is a key determinant of human behavior and has been well documented in the psychological and behavioral economics literature. This paper shows that reciprocity has significant implications for computer agents that interact with people over time. It proposes a model for predicting people's actions in repeated bilateral rounds of interactions. The model represents reciprocity as a tradeoff between two social factors: the extent to which players reward and retaliate others' past actions (retrospective reasoning), and their estimate about the future ramifications of their actions (prospective reasoning). The model is trained and evaluated in a sequence of rounds of negotiation that vary the set of possible strategies at each round as well as players' benefit from potential strategies. Results show that reasoning about reciprocal behavior significantly improves the predictive power of a computer agent that learned to play with people. The agent outperformed other computer learners that did not model reciprocity, or that played various game theoretic equilibria. These results indicate that computers that interact with people need to represent and to learn the social factors that affect people's play when they interact over time.

Introduction

This paper describes a model for dynamic interaction that explicitly represents people's reciprocal reasoning. Our theory formalizes reciprocal behavior as consisting of two factors: Players' retrospective benefit measures the extent to which they retaliate or reward others' actions in the past; players' prospective benefit measures players' reasoning about the ramification of a potential action in the future, given that others are also reasoning about reciprocal behavior. Players' retrospective benefit depends on their beliefs about each others' intentions towards them. These beliefs are explicitly represented in players' utility functions, allowing the model to represent the tradeoff people make between the retrospective and prospective benefit associated with particular actions.

We used a hierarchical model in which the higher level describes the variation between players in general and the lower level describes the variation within a specific player. This captured the fact that people may vary in the degree to which they punish or reward past behavior. We compared the performance of models that reason about reciprocal behavior with those that solely learn the social factors of one-shot scenarios, as well as models that use equilibria concepts from cooperative and behavioral game theory. We show that a model that learned the extent to which people reason about retrospective and prospective strategies was able predict people's play better than the players that did not consider either reciprocal factor, or considered just one of them.

Interaction Scenario

Our experiments deployed a game called Colored Trails (CT) [4]. CT is played on a 4x4 board of colored squares with a set of chips. One square on the board was designated as the goal square. Each player's icon was initially located in a random, non-goal position. Players were issued four colored chips. To move to an adjacent square required surrendering a chip in the color of that square. Players have full view of the board and each others' chips.

Our version of CT included a one-shot take-it-or-leave-it negotiation round between two agents that needed to exchange resources to achieve their goals. Players are designated one of two roles: proposer players could offer some subset of their chips to be exchanged with some subset of the chips of responder players; responder players could in turn accept or reject proposers' offers. If no offer was made, or if the offer was declined, then both players were left with their initial allocation of chips. Players' performance was determined by a scoring function that depends on the result of the negotiation. Players' roles alternated at each round.

While describing a simple negotiation scenario, CT presents decisions to people within a task context that involves deploying resources to accomplish tasks and satisfy goals. Allain [1] has shown that situating decisions within a task context significantly influences human decision-making and has a positive effect on their performance overall.

Model of Interaction

We define an instance to include a set of finite rounds of bilateral play. Each round includes a game consisting of a CT board, chip allocations, and players' initial positions. The game determines the set of possible exchanges that the proposer can offer. The datum for a single round is a tuple consisting of an observed offer made by the proposer player and response made by the responder player.

To capture people's diverse behavior we use the notion of types. A type captures a particular way of making a decision, and there may be several possible types. At each round, the probability of an action depends on players' types as well as on the history of interaction prior to the current round.

The way the interaction history affected players' strategies was encapsulated by a "merit" scalar. Each player's merit was given an initial value of zero at the onset of an instance and is updated by the agents given the observations at each round. A positive merit value for agent i implies that agent j believes that i has positive intentions towards j, and conversely for a negative merit value. This belief depends on the relative difference between the benefit from the proposed offer to agent j and an action deemed ``fair'' to agent j.

The following figure provides a schema of the dependencies that hold between players' interactions in our model. Each node "Merit" refers to a tuple containing the merit scalar for the proposer or responder agent. Each "Type" node generates an observation for the appropriate player.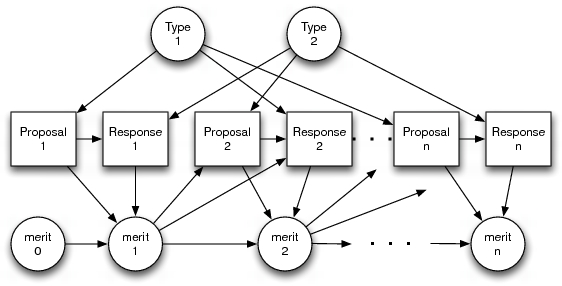

Representing Social Factors

We define the following social factors that affect people's play when they interact with each other over time.

Individual Benefit

This feature represents the immediate benefit to an agent at a round.

Other's Benefit

This feature represents the immediate benefit to the co-participating agent at a round.

Retrospective Benefit

This feature represents the benefit to an agent from rewarding and punishing past actions of the other agent. We define this to be the product of the other's benefit and its merit.

Prospective Benefit

This feature represents the benefit the agent expects to receive in the future as a result of taking its current action. Players' prospective benefit depends on the consequences of their action in future rounds, given that players update their beliefs about each others' types and intentions.

Using and Learning the Model

We wish to learn a mixture model consisting of a distribution over people's types, and the weight values for each type. To this end, we adapt an algorithm proposed by Gal et al. [3] in which gradient descent is used to update the weight after each observation for each type. The likelihood that each type generated an instance can be computed using Bayes rule. We make the degree to which a training example contributes to learning the weights in a network be proportional to the probability that the model actually generated the data. To this end, we assign a learning rate that depends on the likelihood that each type generated a particular instance. We proceed to update the weights for each instance in training set for every agent and for every possible instantiation of each type. In our formalism, this corresponds to summing over the possible types Players' types are unobserved during training, but after each epoch computing the new parameters is done using a variant of the EM algorithm [2].

Results and Discussion

We performed human subject trials to collect data of people playing our dynamic CT scenario. There were ten subjects that generated 54 instances of dynamic interactions. Each instance consisted of between four and ten rounds of CT games in which the players alternated proposer-responder roles at each round. CT games were sampled from a distribution that varied the number of possible negotiation strategies, their associated benefit and the dependency relationships between players, i.e. who needed whom to get to the goal. A total of 287 games were played.

An initial analysis of the data revealed that players engaged in reciprocal behavior when they interacted with each other. For example, a significant correlation was found between the benefit to the responder from one round to the next. This shows that if the proposer was nice to the responder in one round, the responder (who became a proposer in the next round) rewarded the gesture by making a nice offer. Similar correlations were apparent across multiple rounds, suggesting that the effects of reciprocal reasoning on people are long lasting.

We learned several computer models of human players. The model named no-learning used weights learned from data collected from single-shot games. Including this model allowed us to test to what degree behavior from single-shot games carries over to the dynamic setting. The model named no-recip learned only the weights for the individual benefit and other's benefit, without accounting for reciprocal behavior. This model has been shown to capture people's play in one-shot scenarios [3]. The model named recip learned all four features, the two non-time-dependent features and the features representing both retrospective and prospective benefit. The models named retro and prosp learned three features: the two non-time-dependent features, and either the retrospective benefit or the prospective benefit, respectively. We also compared to two game-theoretic concepts: the Nash Bargaining solution [5], and the Fairness Equilibrium [6], which attempts to capture player's psychological benefit from rewarding or punishing others who they think will be nice or nasty to them.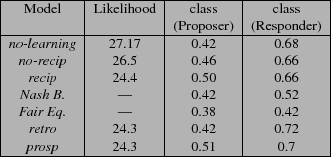

The first column in the results table shows the negative log likelihood of the data. Since the Nash bargaining solution and the fairness equilibrium do not define probability distributions, no likelihood is shown for them. The likelihoods are fairly similar to each other because the probability distribution is relatively flat, because there are a large number of offers available with similar utility. According to this metric, we see that all the models that learn reciprocal behavior do better than the no-recip model which does not. Furthermore, the no-learning model does worst, indicating that we cannot simply reuse the weights learned for a single-shot game. However there is little difference between the three-feature models and the four-feature model (the four-feature model actually doing marginally worse). So there is evidence that people do employ reciprocal reasoning, and that it is useful to model this computationally, but according to this metric this can be captured just as well with a single reciprocal feature, and either retrospective or prospective benefit will do just as well.

Looking more closely at the results provides more information. The next column, labeled "class(Proposer)", indicates the fraction of times that the actual offer made by the proposer was in the top 25% of offers predicted by the model. For the computer models this meant the top 25% in order of probability; for the Nash Bargaining solution this meant the top 25% in order of product of benefits for the proposer and responder; and for the Fairness Equilibrium this meant the top 25% in order of total benefit including psychological benefit. The results for this metric show that recip and prosp perform best, while retro performs as badly as no-learning and the game-theoretic models. This provides evidence that it is prospective benefit that is particularly important. The final column shows a similar metric for the responder decision; in this case it is the fraction of time that the model correctly predicted acceptance or rejection. We see here that the two game-theoretic equilibria did significantly worse than the other models, showing that we cannot simply borrow game-theoretic notions and expect them to work well. There was little differentiation between the other models, with the two three-parameter models doing slightly better. Taking all the metrics into account, we conclude that there is no evidence that people simultaneously reason prospectively and retrospectively, and of the two temporal features prospective reasoning are more important.

References:

[1] A. Allain, The effect of Context on Decision-making in Colored Trails. Undergraduate thesis, Harvard University, 2006.

[2] A.P. Dempster, N.M Laird and D.B. Rubin. Maximum Likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society

[3] Y. Gal, F. Marzo, B.J. Grosz and Avi Pfeffer, Learning social preferences in games. In Proc. 19th National Conference on Artificial Intelligence the Conference, San Jose, CA, July 2004.

[4] B.J. Grosz, S. Kraus, S. Talman and B. Stossel, The Influence of Social Dependencies on Decision-Making. Initial investigations with a new game. In Proc. 3rd International Joint Conference on Multi-agent Systems.

[5] J. Nash, The Bargaining Problem. Econometrica

[6] M. Rabin, Incorporating Fairness into Game Theory and Economics. In American Economic Review