Research Abstracts - 2007

Deformation Transfer for Triangle Meshes

Deformation transfer applies the deformation exhibited by a source triangle mesh onto a different target triangle mesh. Our approach is general and does not require the source and target to share the same number of vertices or triangles, or to have identical connectivity. The user builds a correspondence map between the triangles of the source and those of the target by specifying a small set of vertex markers. Deformation transfer computes the set of transformations induced by the deformation of the source mesh, maps the transformations through the correspondence from the source to the target, and solves an optimization problem to consistently apply the transformations to the target shape. The resulting system of linear equations can be factored once, after which transferring a new deformation to the target mesh requires only a backsubstitution step. Global properties such as foot placement can be achieved by constraining vertex positions. We demonstrate our method by retargeting full body key poses, applying scanned facial deformations onto a digital character, and remapping rigid and non-rigid animation sequences from one mesh onto another.

Deformation transfer copies the deformations exhibited by a source mesh onto a different target mesh. In this example, deformations of the reference horse mesh are transfered to the reference camel, generating seven new camel poses. Both gross skeletal changes as well as more subtle skin deformations are successfully reproduced.

Mesh-Based Inverse Kinematics

The ability to position a small subset of mesh vertices and produce a meaningful overall deformation of the entire mesh is a fundamental task in mesh editing and animation. However, the class of meaningful deformations varies from mesh to mesh and depends on mesh kinematics, which prescribes valid mesh configurations, and a selection mechanism for choosing among them. Drawing an analogy to the traditional use of skeleton-based inverse kinematics for posing skeletons, we define mesh-based inverse kinematics as the problem of finding meaningful mesh deformations that meet specified vertex constraints.

Our solution relies on example meshes to indicate the class of meaningful deformations. Each example is represented with a feature vector of deformation gradients that capture the affine transformations which individual triangles undergo relative to a reference pose. To pose a mesh, our algorithm efficiently searches among all meshes with specified vertex positions to find the one that is closest to some pose in a nonlinear span of the example feature vectors. Since the search is not restricted to the span of example shapes, this produces compelling deformations even when the constraints require poses that are different from those observed in the examples. Furthermore, because the span is formed by a nonlinear blend of the example feature vectors, the blending component of our system may also be used independently to pose meshes by specifying blending weights or to compute multi-way morph sequences.

Top row: Ten lion example poses. Bottom row: A sequence of posing operations. (A) Two handle vertices are chosen. (B) The front leg is pulled forward and the lion continuously deforms as the constraint is moved. (C) The red region is selected and frozen so that the front leg can be edited in isolation. (D) A similar operation is performed to adjust the tail. The final pose is different from any individual example.

Inverse Kinematics for Reduced Deformable Models

Articulated shapes are aptly described by reduced deformable models that express required shape deformations using a compact set of control parameters. Although sufficient to describe any shape deformation, the control parameters can be ill-suited for animation tasks, particularly when reduced deformable models are inferred automatically from example shapes. Our algorithm provides intuitive and direct control of reduced deformable models similar to a conventional inverse-kinematics algorithm for jointed rigid structures. With only a few manipulations, an animator can automatically and interactively pose detailed shapes at rates independent of their geometric complexity. Our resolution-independent metric ensures that even a few vertex constraints generate example-like meshes.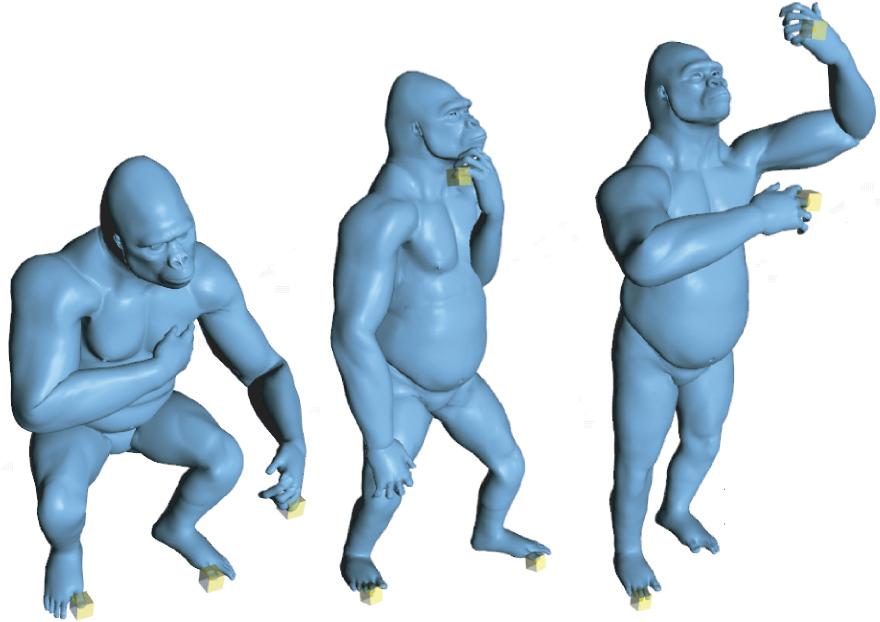

References:

[1] Robert W. Sumner, and Jovan Popović. Deformation Transfer for Triangle Meshes. In ACM Transactions on Graphics 23(3), pp. 399--405, 2004.

[2] Robert W. Sumner, Matthias Zwicker, Craig Gotsman, and Jovan Popović. Mesh-Based Inverse Kinematics. In ACM Transactions on Graphics 24(3), pp. 488--495, 2005.

[3] Kevin G. Der, Robert W. Sumner, and Jovan Popović. Inverse Kinematics for Reduced Deformable Models. In ACM Transactions on Graphics 25(3), pp. 1174--1179, 2006.