Research Abstracts - 2007

Abstract

We study training algorithms for dependency parsing that use marginals derived from log-linear distributions over parse trees. Although the inside-outside algorithm yields these marginals for projective structures, it is not applicable to the non-projective case. We present a novel algorithm for calculating marginals of distributions over non-projective trees, via an adaptation of Kirchhoff's Matrix-Tree Theorem. We explore the use of such marginals in training log-linear models, and in exponentiated-gradient optimization of max-margin models. Empirical results in multilingual dependency parsing show that the proposed algorithms outperform the averaged perceptron.

Overview

Recent work has applied discriminative machine learning methods to the problem of natural language parsing. A key advantage of these methods is their ability to employ rich and flexible features. In particular, discriminative methods have been applied to dependency parsing, with excellent empirical results [1].

One advantage of dependency parsing over constituent parsing is that non-projective structures are easily represented, which is important for some languages such as Czech. McDonald et al. [1] observed that non-projective parses correspond to spanning trees on the words of a sentence. Based on this observation, they introduce an online learning algorithm for non-projective parsing that achieves good performance on non-projective languages.

While online algorithms are easy to implement, and scale well to large datasets, log-linear models [2,3] or max-margin methods [4] often provide better performance. The latter algorithms explicitly minimize the loss incurred when parsing the entire training corpus. We develop a framework for training such models for dependency parsing. We specifically address the theoretical problems associated with the non-projective case, and show how they may be resolved using tools from combinatorial graph theory.

Training algorithms for log-linear models typically rely on the computation of partition functions and marginals; these computations require summations over the space of possible structures. In the case of projective parsing, the partition function and marginals can be evaluated in time using an inside-outside style algorithm [5] for the Eisner [6] parser. However, this approach does not carry over to the non-projective case, which involves enumeration over the set of all spanning trees. As we show here, this enumeration problem can in fact be solved by adapting a well-known result in graph theory: Kirchhoff's Matrix Tree Theorem [7]. A naive application of the theorem yields and algorithms for computation of the partition function and marginals, respectively. However, our adaptation finds the partition function and marginals in time using simple matrix determinant and inversion operations.

The use of marginal computations is not confined to training log-linear models. We also show how the marginals obtained here suffice to train max-margin models for non-projective dependency parsing, via an Exponentiated Gradient (EG) algorithm [8]. The experiments presented here constitute the first application of this algorithm to a large-scale problem.

We applied the marginal-based algorithms to six languages with varying degrees of non-projectivity, using datasets obtained from the CoNLL-X shared task [9]. Our experimental framework compared three training algorithms: log-linear models, max-margin models (using EG training), and the averaged perceptron. Each of these was applied to both projective and non-projective parsing. Our results demonstrate that marginal-based algorithms outperform the perceptron. Furthermore, we find non-projective training approaches typically yield performance that is as good as or better than projective training.

Three Inference Problems for Marginal-based Dependency Parsing

Focus on a single, fixed, sentence 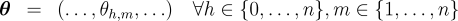and assume that we are given a score vector

that specifies a score for every possible dependency in the sentence. Furthermore, assume that the scores are to be interpreted additively, so that the score for a tree decomposes into a sum over the scores of its dependencies: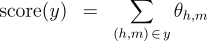

where indicates a head-modifier dependency with head index and modifier index . Note that in a typical linear model for dependency parsing, the scores would be defined in terms of inner products between a parameter vector and feature vector:

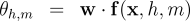Using the score vector, we define a globally-normalized log-linear probability model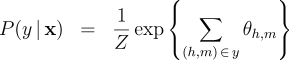

where is the partition function, which normalizes the distribution. We also consider the marginals, which give the probability of any given dependency being active:

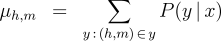We define the following three inference problems in the context of this probability model.

Decoding :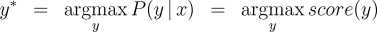

Computation of the Partition Function :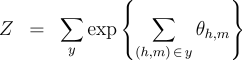

Computation of the Marginals :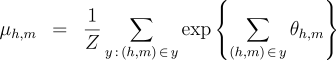

Efficient solutions to these three inference problems are essential for our marginal-based approaches to dependency parsing. First, note that the decoding problem above is equivalent to the basic parsing task. In addition, efficient algorithms for recovering the partition function and marginals suffice to allow gradient-based optimization of globally-normalized log-linear models. Furthermore, efficient computation of the marginals suffices for Exponentiated Gradient [8] optimization of max-margin models.

Non-projective Parsing with the Matrix-Tree Theorem

There are well-known algorithms for efficiently solving all three inference problems in the case of projective dependency parsing. For non-projective parsing, efficient algorithms have only been proposed for the Decoding problem [1]. We show that an adaptation of the Matrix-Tree Theorem yields efficient algorithms for the other two inference problems.

Consider a complete directed graph over the words of the sentence and note that non-projective parses of the sentence correspond to spanning trees of this graph. Suppose that the edges of this digraph are weighted according to the following weighted adjacency matrix: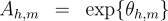

Then, the product of the edge-weights of a spanning tree is proportional to the probability of the corresponding non-projective parse in a globally-normalized log-linear model. Moreover, the constant of proportionality is exactly equal to the partition function: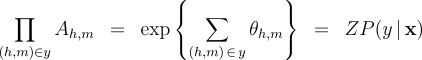

Therefore, the sum of the product of edge weights for all spanning trees of this graph recovers the partition function: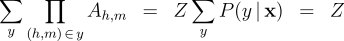

The Laplacian of a graph is a matrix derived from the (possibly-weighted) adjacency matrix of that graph. Kirchoff's Matrix-Tree Theorem relates the sum-product of all weighted spanning trees rooted at some fixed node to the determinant of a submatrix of the graph Laplacian. The partition function is given by the sum-product of all weighted spanning trees rooted at any node, so a straightforward application of the Matrix-Tree Theorem would involve a summation of determinants—i.e., an algorithm. However, we find that the determinant of a modified Laplacian matrix yields the partition function directly, resulting in an algorithm.

In order to recover the marginals efficiently, we apply two identities. First, for a globally-normalized log-linear model, the marginals are given by the partial derivatives of the log partition function: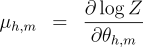

Second, the derivative of the log-determinant of a matrix has a simple form: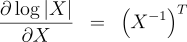

These two identities can be combined via the chain rule, resulting in an algorithm for computing the marginals that is dominated by the matrix inversion operation. Therefore, the marginals can be obtained in time.

Extensions: Multiple Roots and Labels

We briefly mention two extensions to our basic method. First, in some dependency parsing tasks, the desired structures are forests rather than trees—i.e., more than one root node may be allowed. The existing approaches for single-root parsing, both projective and non-projective, can be extended to multiple-root parsing quite naturally.

Second, dependency parsing often involves training and prediction of labeled dependencies, which are tuples of the form 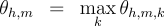, where is the index of a label. The three inference problems are then redefined to incorporate additional maximizations or summations over the set of possible labels. However, because the tree-scoring function completely decouples the labels, the unlabeled algorithms can continue to be applied, modulo some simple preprocessing. Specifically, for the decoding inference problem, it suffices to define

and apply the unlabeled decoding algorithm to the resulting set of dependency scores. Analogously, for the partition function and marginals inference problems, defining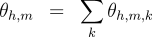

and applying the unlabeled algorithms again suffices.

Multilingual Dependency Parsing Experiments

We used our marginal-based algorithms to train dependency parsers (both projective and non-projective) for six different languages: Arabic, Dutch, Japanese, Slovene, Spanish, and Turkish. Training and test data for these languages were obtained from the CoNLL-X shared task. We evaluated two marginal-based approaches: log-linear models (with Conjugate Gradient training) and max-margin models (with Exponentiated Gradient training). We compared the parsers trained by the marginal-based approaches to baseline parsers that were trained by the averaged perceptron; note that the averaged perceptron is known to be competitive for many tasks. Feature sets and data partitions were identical for all three training algorithms. Our final tests showed that in a cross-linguistic comparison, the marginal-based algorithms produced significantly () better parsers than the averaged perceptron.

Acknowledgements

This work was funded by a grant from the National Science Foundation (DMS-0434222) and a grant from NTT, Agmt. Dtd. 6/21/1998. In addition, A. Globerson is supported by a postdoctoral fellowship from the Rothschild Foundation - Yad Hanadiv.

References:

[1] R. McDonald, K. Crammer, and F. Pereira. Online large-margin training of dependency parsers. In Proceedings of ACL, 2005.

[2] M. Johnson, S. Geman, S. Canon, Z. Chi, and S. Riezler. Estimators for stochastic unification-based grammars. In Proceedings of ACL, 1999.

[3] J. Lafferty, A. McCallum, and F. Pereira. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. In Proceedings of ICML, 2001.

[4] B. Taskar, C. Guestrin, and D. Koller. Max-margin markov networks. In NIPS, 2004.

[5] J. Baker. Trainable grammars for speech recognition. In 97th meeting of the Acoustical Society of America, 1979.

[6] J. Eisner. Three new probabilistic models for dependency parsing: An exploration. In Proceedings of COLING, 1996.

[7] W. Tutte. Graph Theory. Addison-Wesley, 1984.

[8] P. Bartlett, M. Collins, B. Taskar, and D. McAllester. Exponentiated gradient algorithms for large-margin structured classification. In NIPS, 2004.

[9] S. Buchholz and E. Marsi. CoNLL-X shared task on multilingual dependency parsing. In Proceedings of CoNLL-X, 2006.