Research Abstracts - 2007

Overview

We apply the dead-end elimination (DEE) strategy from protein design as a preconditioner for the max-flow/min-cut formulation of the image segmentation problem. DEE combines aspects of constraint propagation and branch-and-bound to eliminate solutions incompatible with global optimization of the objective function. Though DEE can be used for segmentation into an arbitrary number of regions, here we evaluate only the binary case. Preliminary results show that DEE consistently reduces the search space for the Edmonds-Karp (EK) min-cut algorithm [2]; tuning DEE for Boykov-Kolmogorov (BK) [3] and other algorithms is future work.

What is Dead-End Elimination?

DEE is a strategy used in computational protein design for the combinatorial optimization problem of assigning amino acids at protein positions, s.t. the energy of a desired protein structure is minimized.[4][5] Consider the objective function

where the first term is the sum of the self-energies for each position's assignment, and the second term is the sum of the pairwise energies for pairs of assignments. For two specific assignments i_a and i_b, if

then i_a cannot be part of the global minimum solution and can be eliminated from the space.

Application to Image Segmentation

The min-cut segmentation problem was reformulated for DEE; the number of positions is the number of pixels, and, for the binary case, there are only two possible assignments (foreground, background) per pixel. We assume that each pixel has a constant number of neighbors, so a sparse DEE implementation can be used, and the runtime is linear w.r.t. the number of pixels and the number of neighbors. The special form of the energy function here allowed us to use a less general, faster form of DEE that has a simple graph interpretation.

Figure 1: We compared the performance of two segmentation algorithms (EK and BK) alone and preceded by DEE. All four methods produced identical segmentations on a set of natural images; two are shown at left. DEE greatly reduced the search space, regardless of the quality of the final segmentation. Two simple energy functions were used; optimizing them was not the focus of this work.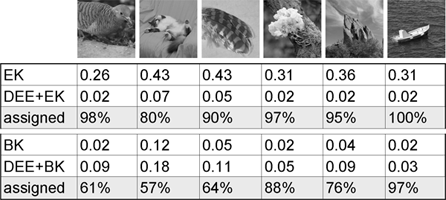

Table 1: Here we show the running times (in seconds) for EK on 50x50 images, for BK on 500x500 images, and for EK and BK with the DEE preconditioner. Times do not include time to compute and read in initial graph weights from file. Also shown is the percentage of pixels that DEE was able to assign in each case.

Figure 2: (Left) Eliminating power (the fraction of pixels assigned by DEE) as a function of image size. (Middle) Eliminating power as a function of the dominance of the pairwise pixel energies in the objective function. DEE's performance can highly depend on the strength of the pairwise terms relative to the self terms. (Right) Running time (averaged over 3 trials) of DEE as a function of image size, for one DEE singles iteration; this includes time to make the new graph to pass onto the BK algorithm.

Potential Future Utility of DEE in Image Segmentation

• With optimized code, might speed up the BK binary segmentation.
• Can potentially be applied to multiway cut problems to reduce search space before using IP/Branch-and-Bound. DEE heuristics/extensions from protein design (DEE pairs, split singles, etc.) can be imported to this problem.
• Is not restricted to graph-representable energy functions; can work with any pairwise-boundable (most commonly, pairwise additive) energy function.

Acknowledgements

Implementation advice from Michael Altman and comments from Vladimir Kolmogorov, Sylvain Paris, and Bruce Tidor helped improve the ICIP paper. We thank David Karger for suggesting a simplified interpretation of the heuristic and Frédo Durand for input images. The authors were supported by a DOE CSGF fellowship under grant number DE-FG02-97ER25308 and a National Science Foundation graduate fellowship.

References:

[1] M. L. Radhakrishnan and S. L. Su. Dead-End Elimination as a Heuristic for Min-Cut Image Segmentation. In Proceedings of the 13th IEEE International Conference on Image Processing, Atlanta, GA, October 2006.

[2] J. Edmonds and R. Karp. Theoretical Improvements in Algorithmic Efficiency for Network Flow Problems, Journal of the ACM, vol. 19, no. 2, April 1972.

[3] Y. Boykov and V. Kolmogorov. An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Computer Vision, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 26, no. 9, September 2004.

[4] J. Desmet, M. De Maeyer, B. Hazes, and I. Lasters. The Dead-end Elimination Theorem and its Use in Protein Sidechain Positioning, Nature, vol. 356, April 1992.

[5] R. F. Goldstein. Efficient Rotamer Elimination Applied to Protein Side-chains and Related Spin Glasses, Biophysics Journal, May 1994.