Lynne Salameh, Varun Aggarwal & Una-May O'Reilly

WHAT?

Circuit optimization has primarily taken two directions, first that of stochastic black-box optimization with SPICE-based evaluations [1] (also known as simulation-based approach) and second, that of expressing the circuit as equations which are then plugged into a geometric program solver [2]. The former requires little effort and time from the circuit designer who only has to setup SPICE scripts for performance measurement of the circuit and to choose which variables are optimized. However, the optimization is slow since SPICE is invoked in-loop for every iteration of the optimization and there is no exploitation of the knowledge of the particular circuit being optimized. Also, blackbox optimization gives no guarantee of finding the global optima. The latter approach, that of equation based optimization using geometric programming, requires effort and time on part of the designer to write accurate equations for the circuit. Once the equations are written, very fast interior point algorithms are used to find the global optima. Though the optimization algorithm guarantees global optimization, the inaccuracy in the optimization is due to inaccurate circuit equations and transistor models. These inaccuracies and the requirement of expressing models in the form of posynomials can be prohibitive.

Given the above scenario, the industry has adopted black-box optimization as a tool-based approach, where the designer can use a blackbox optimization tool to size any circuit he/she wants. This approach is prohibitive for very large circuits. Geometric Programming has shown some acceptance as an IP-based approach, where geometric programs for particular circuits (popularly called IP in semiconductor industry) are written and these circuits can be very quickly optimized/ported to a new technology. Extension to new circuits is not straightforward and requires time and effort.

In the state-of-art, the dominating problem with geometric programming is the inaccuracy of the transistor models and that of circuit equations, which leads to inaccurate optimization. We are interested in addressing the former by building accurate posynomial models for transistors. The simple square-law model for MOS yields monomial parameters, however the transistor doesn't accurately follow the square law. Moreover, with the shrinking technology, transistor behavior has become more unpredictable and BSIM transistor model has more than 50 parameters for fitting to fabrication data. The transition from weak inversion to strong inversion adds another dimension of complexity obviously not captured in the square law.

The current methods for posynomial creation are the following: i. Generation of monomial models [3], ii. Generation of posynomial models with integer-valued coefficients [4,5] (with local-hill climbing for fractional coefficients [6]), iii. Piece-wise monomial fitting [7]. None of these approaches can generate or be principally extended to produce a posynomial with real-valued exponents and variable number of terms. Also, transistor parameters, for instance gm, have fractional powers even with square-law model. Thus posynomial with integer-valued powers seems inappropriate.

We want to explore methods to generate variable-term posynomials with real-valued exponents to improve the accuracy of the transistor models.  We shall then measure the gain in the accuracy of the optimization when these more accurate models are used in the geometric programming flow.

HOW?

In principle, posynomial generation is a regression problem where the polynomial can have real-valued exponents and is restricted to have only positive coefficients. We have devised an algorithm to generate posynomials which is a hybrid of a genetic algorithm and a convex optimization algorithm [8] (linear programming/quadratic programming). The genetic algorithm searches in the space of exponents, while the convex optimizer searches in the space of coefficients. This is depicted in Figure 1. The algorithm also uses cross-validation to ensure good model generalization.

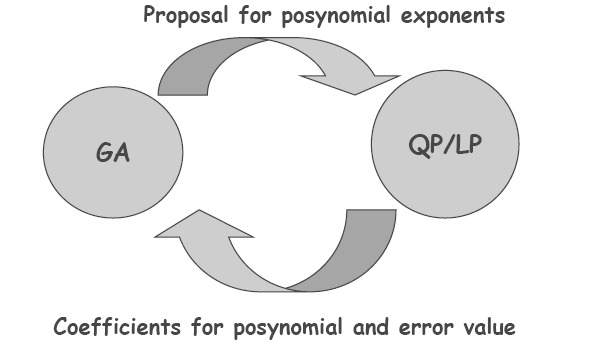
Figure 1

We have shown that the models produced by the technique are superior to several published techniques [9]. The technique is a general technique to fit posynomial models to any kind of data and is extensible to different error metrics easily. We are currently working with industry-partners to ascertain the improvement in the optimization results due to use of more accurate models. We are also exploring combining other machine learning techniques such as boosting, bagging and bootstrapping data  with our algorithm for improving model accuracy,

References:

[1] B. D. Smedt and G. Gielen. WATSON: Design space boundary exploration and model generation for analog and RF IC design. IEEE Trans. on CAD of Int. Circuits and Systems,22(2):213-224, 2003.

[2] M. Hershenson, S. S. Mohan, S. P. Boyd, and T. H. Lee. Optimization of inductor circuits via geometric programming. In DAC, pages 994-998, New York, NY, USA, 1999. ACM Press.