Introduction

An increasing range of problems in Artificial Intelligence and Computer Science involve finding optimal solutions to problems that involve a rich combination of logical and algebraic constraints, and require a hybrid coupling of logical decision techniques with mathematical optimization to solve. Examples include planning with resources, autonomous vehicle control and verification of timed and hybrid systems. Focusing on the area of autonomous vehicle control, deep space explorers must choose between tasks and temporal orderings, while optimizing flight trajectories for fuel usage. On Earth, search and rescue units must construct and compare different vehicle trajectories around dangerous areas, such as a fire, on the approach to a trapped individual.Each of these tasks involves designing an optimal state trajectory, based on a continuous dynamic model. At some point, they must satisfy additional logical constraints, such as mission tasks, task orderings and obstacle avoidance.

These Hybrid Logic/Optimization Problems (HLOPs) can be formulated in three ways: first, by introducing integer variables and corresponding constraints to Linear Programming (LP), known as Mixed Integer Programming (MIP) as in [1][2]; second, by augmenting LP with propositional variables so that the propositional variables can be used to “trigger” linear constraints, known as Mixed Logic Linear Programming (MLLP) in [3] and LCNF in [4]; third, by extending LP with disjunctions, without adding any variables or constraints, called Disjunctive Programming (DP) as in [5].

Currently the typical way of solving HLOPs is to formulate them in MIP and solve them using Branch & Bound (B&B), as seen in Figure 1. However, this is not efficient for solving large and "hard" ([6]) problems, such as real-time path planning problems. The reasons are the following:

1. The MIP formulation enlarges the problem dimension by adding overhead integer variables and corresponding constraints to represent logical decisions.
2. B&B prunes subsets of the search tree that correspond to relaxed subproblems that it identifies as inconsistent or sub-optimal, but the information of solving such subproblems is lost when they are pruned.

Figure 1. Pseudo code for Branch & Bound

Our goal is to develop an efficient algorithm to overcome the above drawbacks, based on [7]. We formulate HLOPs in DP, which combines the expressive power of propositional logic with that of LP, without the overhead of additional variables or constraints.Our approach builds upon B&B, and introduces generalized conflict learning and forward conflict-directed search to utilize the information that is lost in B&B in order to speed up the search.

Problem Formulation

We use disjunctive programs to effectively capture both the continuous dynamics and control decisions present in hybrid logic/optimization problems. Figure 2 depicts a simple example of an HLOP, introduced in [1]. Eq. (1) describes its DP formulation. In particular, a vehicle has to go from point A to C, without hitting the obstacle B, while minimizing the fuel use.

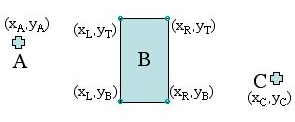
Figure 2. A simple example of an HLOP

In Eq. (1), V denotes logical or, x is a vector of decision variables that includes, at each time step i (=1,…,n), the position, velocity and acceleration of the vehicle; f(x) is a linear

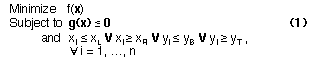
cost function in terms of fuel use; g(x) ≤ 0 is a conjunction of linear constraints on vehicle dynamics, and the last constraint keeps the vehicle outside obstacle B at each time step i. In general, DP takes the form shown in Eq. (2):

where x is a vector of decision variables, f(x) is a linear cost function, and the constraints are a conjunction of n clauses, each of which (clause i) is a disjunction of mi linear inequalities, Cj(x) ≤ 0. DP reduces to a standard LP in the special case when mi=1, for all i=1,…,n. In comparison with MIP, DP adds no overhead variables or constraints to represent logical decisions.

Overall Approach

Our approach has three key features: First, generalized conflict learning, which learns qualitative abstractions (conflicts) comprised of constraint sets that produce either infeasibility or sub-optimality; Second, forward conflict-directed search, which heuristically guides the forward step of the search away from regions of state space corresponding to known conflicts; Third, induced unit clause relaxation, which forms a relaxed problem from a subset of the unit clauses that are induced from the original problem.

Recall in Branch & Bound, when a subproblem is found infeasible or sub-optimal, it and its subtree are pruned. We, however, extract the source of the infeasibility or sub-optimality before pruning, called a conflict, so that this information can be used to guide the search. A conflict can be of two types: (1) an irreducible set of constraints that is learned from infeasibility, or (2) an irreducible set of constraints that is learned from sub-optimality. A set of constraints is irreducible if removing any one of the constraints from the set resolves the infeasibility or sub-optimality. Note that there can be more than one irreducible sets (possibly with different cardinalities) involved in one infeasibility or sub-optimality, and a type-1 or type-2 conflict is not guaranteed to have the minimal cardinality. Hence the name irreducible instead of minimal. An infeasibility conflict (type 1) is an irreducible subset of the inconsistent constraints of an infeasible sub-problem. An example is the constraint set {a,c,d} in Figure 3(b). The subproblem in Figure 3(a) is infeasible, but its constraint set is not an infeasibility conflict, as a proper subset of it, as in Figure 3(b), remains inconsistent.

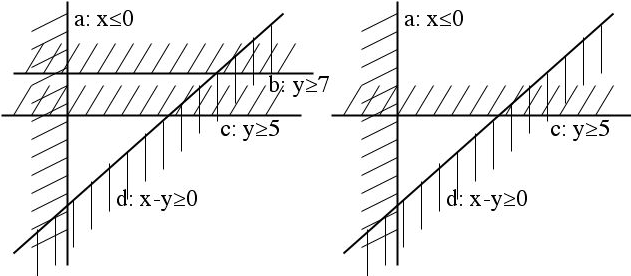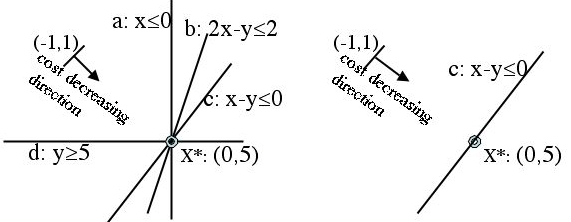Figure 3(a). An infeasible subproblem: constraint set {a,b,c,d}is not consistent.	(b). After removing constraint b, it is still infeasible.	Figure 4(a). The optimal solution is X*. Constraints a, b, c and d are all active.	(b). After removing constraints a, b and d, X* stays the same.

An active constraint of a feasible problem S, is a constraint that takes equality at S’s optimal solution x*. A sub-optimality conflict (type 2) is an irreducible subset of the active constraints of a feasible subproblem whose optimal solution is not better than the incumbent. An example is the constraint set {c} in Figure 4(b). All the constraints are active in Figure 4(a), but the set {a,b,c,d} is not a sub-optimality conflict, as it can be reduced to Figure 4(b) without affecting the optimal solution x*. We have proven that both types of conflicts can be obtained efficiently using the LP dual method.

The forward conflict-directed search heuristically guides the forward step of the search away from regions of the feasible space that are ruled out by known conflicts. Traditionally, conflicts are used in the backward step, such as dependency-directed backtracking [8], backjumping [9], conflict-directed backjumping [10], dynamic backtracking [11] and LPSAT [4]. These backtrack search methods use conflicts to select backtrack points. In contrast, we use conflicts in forward search, to move away from known “bad” states. We generalize this idea to guiding B&B away from regions of state space that the known conflicts indicate are infeasible or sub-optimal.

Relaxation is an essential tool for quickly characterizing a problem when the original problem is hard to solve directly; it provides bounds on feasibility and the optimal value of a problem, which are commonly used to prune the search space. Previous research [12] typically solves Disjunctive Programs by reformulating them as Mixed Integer Programs, in which binary integer variables are used to encode the disjunctive constraints. A relaxed problem for a MIP consists of the continuous relaxation of the integer constraints. An alternative way of creating a relaxed LP is to operate on the DP encoding directly, by removing all non-unit clauses from the DP (a unit clause is one that contains a single constraint). Prior work argues for the reformulation of DP as MIP relaxation, with the rationale that it allows the solver to use continuous relaxation on the (binary) integer variables, in contrast to ignoring the non-unit clauses. However, this benefit is at the cost of adding integer variables and constraints, which can significantly increase the dimensionality of the search problem. This cost is not incurred by the DP relaxation. Our approach starts with the direct DP relaxation, and overcomes the weakness of standard DP relaxation (loss of non-unit clauses) by adding to the relaxation additional unit clauses that are logically entailed by the original DP.

Preliminary Results

In the experiments, we programmed our approach and MIP B&B in JAVA, and made comparison on both computation time and memory use. Test problems were generated using a model-based temporal planner, performing multi-vehicle search and rescue missions. This planner takes as input a temporally flexible state plan, which specifies the goals of a mission, and a continuous model of vehicle dynamics, and encodes them in DP. Our solver generates an optimal vehicle control sequence that achieves the constraints in the temporal plan. Results demonstrated an order of magnitude speed-up over MIP B&B.

Acknowledgements 

This research is supported in part by The Boeing Company under contract MIT-BA-GTA-1, and by the NASA grant under contract NNA04CK91A.

References:

[1] T. Schouwenaars, B. De Moor, E. Feron, J. How.,T Mixed integer programming for multi-vehicle path planning. European Control Conference, 2001.

[2] T. Vossen, M. Ball, A. Lotem, D. Nau. On the use of integer programming models in AI planning. IJCAI, 1999.

[3] J.N.Hooker and M.A.Osorio. Mixed Logical/Linear Programming. Discrete Applied Mathematics 96-97 395-442, 1999.

[4] Wolfman and D. Weld. The LPSAT engine & its application to resource planning. IJCAI, 1999.

[5] E. Balas. Disjunctive programming, Annals of Discrete Mathematics 5 3-51, 1979.

[6] D. Mitchell, B. Selman, H. Levesque. Hard and easy distributions of SAT problems. AAAI, 1992.

[7]R. Krishnan. Solving Hybrid Decision-Control Problems Through Conflict-Directed Branch & Bound. M.Eng. Thesis. MIT. 2004.

[8] R. Stallman and G. J. Sussman. Forward reasoning and dependency-directed backtracking in a system for computer-aided circuit analysis, Artificial Intelligence 9 135–196, 1977.

[9] J. Gaschnig Experimental Case Studies of Backtrack vs. Waltz-type vs. New Algorithms for Satisficing Assignment Problems. The 2nd Canadian Conference on AI 268-277, 1978.

[10] P. Prosser. Hybrid algorithms for the constraint satisfaction problem, Computational Intelligence 3, 268–299, 1993.

[11] M. Ginsberg, Dynamic backtracking, Journal of Artificial Intelligence Research 1 25–46, 1993.

[12] J.N.Hooker, Logic, optimization and constraint programming, INFORMS J. on Computing 14 295-321, 2002.