Overview

Autonomous control of dynamic systems has application in a wide variety of fields, from managing a team of agile unmanned aerial vehicles (UAVs) for fire-fighting missions, to controlling a Mars life support system. The control of such systems is challenging for several reasons. First, they are under-actuated systems, which means they are under-actuated (not all state variables are directly controllable). Second, their models involve continuous dynamics described by differential equations. Third, controlling these systems usually requires tight synchronization, and, fourth, the controller must be optimal and robust to disturbances.

An autonomous controller for agile systems should, therefore, provide three capabilities:

1. To handle tight coordination, the system should execute a temporal plan specifying temporal coordination constraints.
2. To deal with under-actuated systems, the controller should elevate the interaction with the system under control (the plant) to the level at which the systems appear directly controllable. The human operator should be able to robustly program the plant in terms of desired state evolution, including state variables that are not directly controllable.
3. To allowin robust control over the system, the intended state evolution should be specified in a temporally flexible manner.

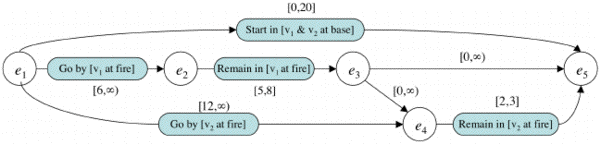
We are developing a model-based executive that enables coordinated control of agile systems, through model-based execution of temporal plans. We introduce the concept of a temporally flexible state plan to express desired system state evolution. An example is illustrated in Fig. 2. Our approach is novel with respect to three aspects. First, we provide a general method for encoding both the temporal state plan and the dynamics of the system as a mixed discrete-continuous mathematical program. Solving this program provides time-optimal trajectories in the plant state space, that satisfy the system dynamics and achieve the state plan. Second, to achieve efficiency and robustness, we extend Model Predictive Control (MPC) [3] to continuous temporal plan execution, in order to design control trajectories for under-actuated, dynamical systems. MPC allows us to achieve tractability, by reasoning over a limited receding horizon, and allows continuous adaptation to disturbances and anomalies. Third, in order to further reduce the complexity of the program and solve it in real time, we use pruning policies that enable us to ignore some of the constraints in the state plan outside the current planning horizon.

Problem Statement and Example

Given a dynamic system (a plant) described by a plant model, and given a temporally flexible state plan, specifying the desired evolution of the plant state over time, the continuous model-based execution (CMEx) problem consists of designing a control sequence that produces a plant state evolution that is consistent with the state plan.

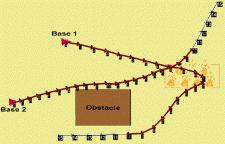
Consider an example involving two fire-fighting Unmanned Air Vehicles (UAVs); in this example, the plant consists of two fixed-wing UAVs. The vehicles evolve in an environment (Fig. 1) involving a reported fire that the team is assigned to extinguish. To do so, they must navigate around unsafe regions (e.g. obstacles) and drop water on the fire. They must also take pictures after the fire has been extinguished, in order to assess the damage. An English description for the mission's state plan (Fig. 2) is:

Vehicles v₁ and v₂ must start at their respective base stations. v₁ (a water tanker UAV) must reach the fire region and remain there for 5 to 8 time units, while it drops water over the fire. v₂ (a reconnaissance UAV) must reach the fire region after v₁ is done dropping water and must remain there for 2 to 3 time units, in order to take pictures of the damage. The overall plan execution must last no longer than 20 time units.

Overall Approach

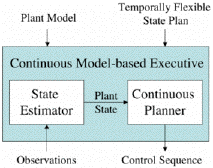
To solve the CMEx problem, we introduce a continuous model-based executive, which takes in a temporally flexible state plan and observations, and reasons on a model of the plant in order to design control sequence that achieve the state plan. The executive consists of a state estimator and a continuous planner (Fig. 3). The continuous planner takes in a state plan, and generates optimal control sequences, based on the plant model, and state sequences provided by the state estimator, which reasons on sensor observations and on the plant model in order to continuously track the state of the plant. Current work on hybrid estimation [1] provides a framework for the state estimator; in this work, we focus on developing an algorithm for the continuous planner.

Previous model-based executives, such as Titan, focus on reactively controlling discrete-event systems [2]. Our approach differs in that it consists of planning into the future, in order to perform optimal, safe execution of temporal plans for systems with continuous dynamics. However, solving the whole CMEx problem over an infinite horizon would present two major challenges. First, the problem is intractable in the case of long-duration missions. Second, it would require perfect knowledge of the state plan and the environment beforehand; this assumption does not always hold in real-life applications such as our fire-fighting scenario, in which the position of the fire might precisely be known only once the UAVs are close enough to the fire to localize it. Furthermore, the executive must be able to compensate possible drift, due to approximations or errors in the plant model.

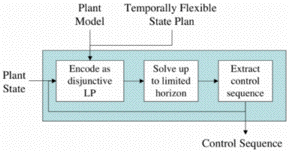
Model Predictive Control (MPC), also called Receding Horizon Control, is a method, introduced in [3], that tackles these two challenges in the context of low-level control (rather than plan-driven control) of systems with continuous dynamics [4]. MPC solves the control problem up to a limited planning horizon, and re-solves it when it reaches a shorter execution horizon. This method makes the problem tractable by restricting it to a small planning window; it also allows for on-line, robust adaptation to disturbances. In this work, we extend MPC to continuous model-based execution of temporal plans by introducing a receding horizon continuous model-based executive. The architecture for our model-based executive is presented in Fig. 4.

As introduced in Fig. 4, we solve the CMEx problem by encoding it over a limited planning horizon as a disjunctive linear program (DLP) [5]. A DLP is an optimization problem with respect to a linear cost function over decision variables, subject to constraints that can be written as logical combinations of linear inequalities. We currently solve DLPs by reformulating them as Mixed-Integer Linear Programs; however, we are also developing methods for solving DLPs directly [6][7].

In order to make the DLP tractable and to solve it in real time, we use pruning policies that enable us to remove from the DLP those constraints that are out of reach during the planning horizon. For instance, constraints relative to collision avoidance between a UAV and an obstacle can be pruned if the vehicle is too far from the obstacle to reach it within the planning horizon. We also use pruning policies to ignore state plan constraints that are provably beyond the horizon.

Preliminary Results

The model-based executive has been implemented in C++, using Ilog CPLEX to solve the DLPs. It has been demonstrated on a range of fire-fighting scenarios on a hardware-in-the-loop testbed, comprised of CloudCap autopilots controlling a set of fixed-wing UAVs. This offers a precise assessment of real-time performance on UAVs. Fig. 1 was obtained from a snapshot of the operator interface, and illustrates the trajectories corresponding to our example.

A preliminary performance analysis demonstrates that the model-based executive is able to design control sequences in real-time for a team of two UAVs, and that the use of constraint pruning policies offers about one order of magnitude speed up in performance.

Acknowledgments

This research is supported in part by The Boeing Company under contract MIT-BA-GTA-1, and by the Air Force Research Lab award under contract F33615-01-C-1850.

References

[1] Hofbaur, M. W. and Williams, B. C.. Hybrid Estimation of Complex Systems. In IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics, 2004.

[2] B. C. Williams, Michel Ingham, Seung H. Chung, and Paul H. Elliott. Model-based Programming of Intelligent Embedded Systems and Robotic Space Explorers. In Proceedings of the IEEE: Special Issue on Modeling and Design of Embedded Software, vol. 9, no. 1, pp. 212--237, January 2003.

[3] J. Richalet, A. Rault, J.L. Testud and J. Papon. Algorithmic control of industrial processes. In Proceedings of the 4th IFAC Symposium on Identification and System Parameter Estimation, pp 1119--1167, 1976.

[4] John Bellingham, Arthur Richards and Jonathan How. Receding Horizon Control of Autonomous Aerial Vehicles. In Proceedings of the American Control Conference, 2002.

[5] Egon Balas. Disjunctive programming. In Annals of Discrete Mathematics, vol 5, pp 3--51, 1979.

[6] Raj Krishnan. Solving Hybrid Decision-Control Problems Through Conflict-Directed Branch and Bound. Master's Thesis, MIT, 2004.

[7] Refer to Hui Li's research abstract.

[8] Phil Kim, Brian C. Williams and Mark Abramson. Executing Reactive, Model-based Programs through Graph-based Temporal Planning. In Proceedings of the International Joint Conference on Artificial Intelligence, 2001.

[9] J. Kennell. Generative Temporal Planning with Complex Processes. M. Eng. Thesis, Massachusetts Institute of Technology, October 2003.

[10] I. Shu. Enabling Fast Flexible Planning through Incremental Temporal Reasoning. M. Eng. Thesis, Massachusetts Institute of Technology, September 2003.